Unconfined Aquifer

Problem description

An aquifer is called an unconfined or phreatic aquifer if its upper surface (water level) is accessible to the atmosphere through permeable material. In contrast to a confined aquifer, the groundwater level in an unconfined aquifer does not have a superimposed impermeable rock layer to separate it from the atmosphere.

To simplify the problem of unconfined flow and to make it analytically writeable, Dupuit (1857) used the following assumptions, now commonly referred to as Dupuit-assumptions, in connection with unconfined aquifers:

• the aquifer lower limit is a horizontal plane;
• the groundwater flow is only horizontal and has no vertical hydraulic component;
• the horizontal component of the hydraulic gradient is constant with the depth and equal to the slope of the groundwater level;
• there is no Seepage.

Using the assumptions of Dupuit, Forchheimer (1898) developed a differential equation for the unconfined steady-state case, and Boussinesq introduced the unconfined transient groundwater flow equation in 1904:

$$ \begin{eqnarray} \frac{∂}{∂x}(h\frac{∂h}{∂x})+\frac{∂}{∂y}(h\frac{∂h}{∂y}) = \frac{S_y}{K}\frac{∂h}{∂t} \label{Boussinesq} \end{eqnarray} $$

where $h[m]$ is the hydraulic head, $S_y$ is the specific yield and $K$ is the hydraulic conductivity. The Specific Yield $S_y$, also known as the drainable porosity, is a quantity that is smaller or equal to the effective porosity in a coarse and porous medium. $S_y$ indicates the volumetric water content that can flow out from the material under the influence of gravity.

The examples shown here are horizontal 2D models parameterized by hydraulic head $h[m]$.

Since the formulation within OGS is basically based on pressure ($P$) and permeability ($k$), the following relationships must be considered during parameterization in order to be able to work head-based and with hydraulic conductivity ($K$):

$$ \begin{eqnarray} P= ρ g h \label{Pressure vs. head} \end{eqnarray} $$ $$ \begin{eqnarray} K= \frac{kgh}{μ} \label{K & k} \end{eqnarray} $$

For the model parameterization this means:

• Gravity must be switched off: g=0
• The density gets the value 1: ρ=1
• The viscosity gets the value 1: μ=1

Note: in such a case, the result is also an output of hydraulic head in [m] and not Pressure in [Pa].

Examples

The following simple examples, which have been compared with MODFLOW simulations, shall verify the result and demonstrate the basic parameterization.

The basic scenario for the two-dimensional unconfined aquifer:

• The area is 9800 m long, 5000 m wide.
• In the East and West, the boundary is conditioned by "no flow" zones.
• The material is a homogeneous coarse-grained sand with an isotropic hydraulic conductivity of 160 m/day (0.00185 m/s).
• The aquifer thickness is 25m.

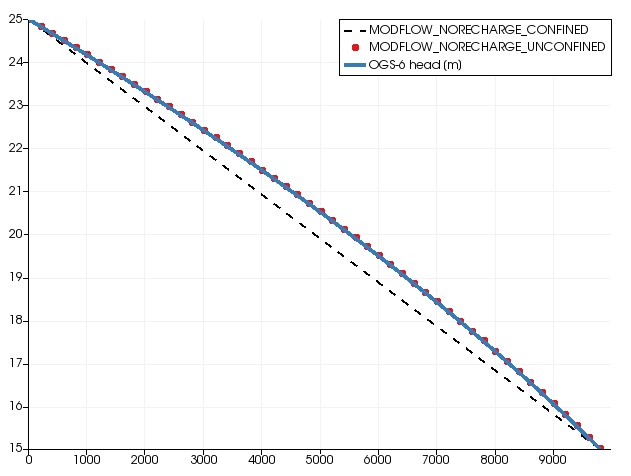
Scenario A

• Steady-state model.
• In the north there is a fixed head boundary condition with 15 m.
• The southern boundary has a fixed head boundary condition with 25 m.
• the Specific Yield is set to $S_y = 0.0$

  

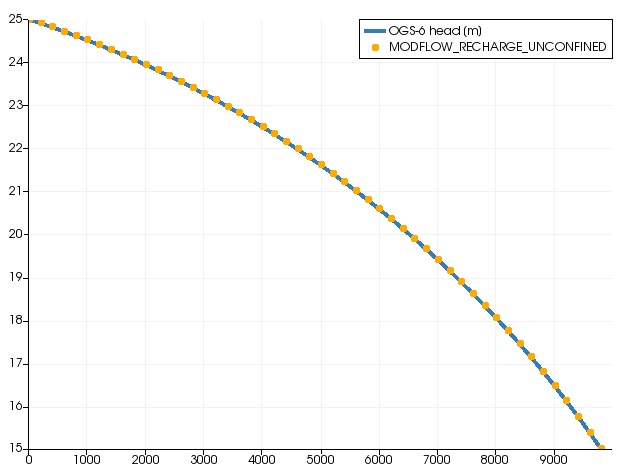
Scenario B

• Like scenario A and additionally
• with an average groundwater recharge rate = 3.54745E-09 m/s

  

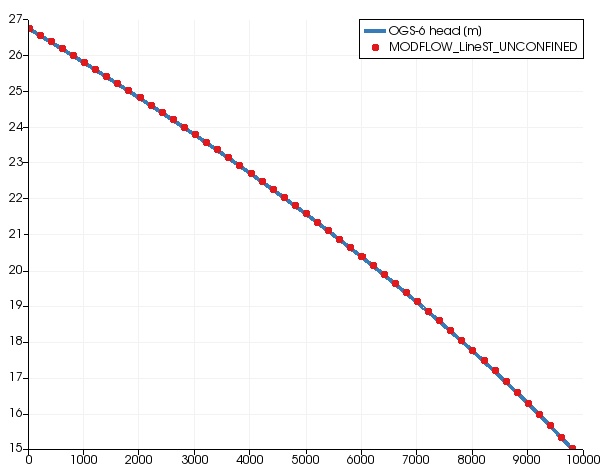
Scenario C

• like scenario A but
• with an inflow rate of 4.62963E-05 m3/s per meter at the southern boundary

  

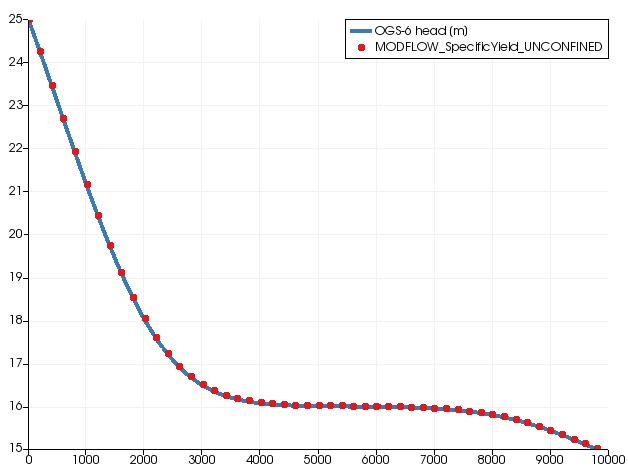
Scenario D

• like scenario A but transient and
• with a Specific Yield $S_y_ = 0.25$.
• Simulation time = 100 days.

  

References

For more information see e.g.

• Boussinesq J. Recherches th´eoriques sur l’´ecoulement des nappes d’eau infiltr´ees dans le sol 445 et sur le d´ebit des sources. J. Math´ematiques Pures Appliqu´ees, 10(5–78):363–394, 1904.
• Diersch HJG. FEFLOW Finite Element Modeling of Flow, Mass and Heat Transport on Porous Media. Berlin, Heidelberg: Springer-Verlag; 2014. Finite Element Modeling of Flow, Mass and Heat Transport in Porous and Fractured Media 2014.
• Dupuit J. Mouvement de l’eau a travers le terrains permeables. C. R. Hebd. Seances Acad. Sci., 45:92–96, 1857.
• Forchheimer P. Über die Ergiebigkeit von Brunnenanalgen und Sickerschlitzen. Z. Architekt. Ing. Ver. Hannover, 32:539–563, 1886.
• Forchheimer P. Grundwasserspiegel bei Brunnenanlagen. Z. Osterreichhissheingenieur Architecten Ver, 44:629–635, 1898.
• Kolditz, O., Görke, U.-J., Shao, H., Wang, W.: Thermo-Hydro-Mechanical-Chemical Processes in Porous Media - Benchmarks and Examples, Lecture Notes in Computational Science and Engineering, 2012.
• Mishra P.K., Kuhlman K.L. (2013) Unconfined Aquifer Flow Theory: From Dupuit to Present. In: Mishra P., Kuhlman K. (eds) Advances in Hydrogeology. Springer, New York, NY 2013.