Theis' problem

• Parabolic/LiquidFlow/AxiSymTheis/axisym_theis.prj

Problem description

Theis’ problem examines the transient lowering of the water table induced by a pumping well. Theis’ fundamental insight was to recognize that Darcy’s law is analogous to the law of heat flow by conduction, i.e., hydraulic pressure being analogous to temperature, pressure-gradient to thermal gradient.

The assumptions required by the Theis solution are:

• the aquifer is homogeneous, isotropic, confined, infinite in radial extent,
• the aquifer has uniform thickness, horizontal piezometric surface
• the well is fully penetrating the entire aquifer thickness,
• the well storage effects can be neglected,
• the well has a constant pumping rate,
• no other wells or long term changes in regional water levels.

Analytical solution

The analytical solution of the drawdown as a function of time and distance is expressed by

$$ \begin{eqnarray} h_0 - h(t,x,y) = \frac{Q}{4\pi T}W(u) \label{theis} \end{eqnarray} $$ $$ \begin{eqnarray} u = \frac{(x^{2}+y^{2})S}{4Tt} \label{theis_u} \end{eqnarray} $$

where $h_0$ is the constant initial hydraulic head $[L]$, $Q$ is the constant discharge rate [$L^{3}T^{-1}$], $T$ is the aquifer transmissivity [$L^{2}T^{-1}$], $t$ is time $[T]$, $x,y$ is the coordinate at any point $[L]$ and $S$ is the aquifer storage $[-]$. $W(u)$ is the well function defined by an infinite series for a confined aquifer as

$$ \begin{eqnarray} W(u) = -\gamma -lnu + \sum^{\infty}_{k=1}{\frac{(-1)^{k+1}u^k}{k\cdot k!}} \label{theis_wu} \end{eqnarray} $$

where $\gamma\approx$ 0.5772 is the Euler-Mascheroni constant. For practical purposes, the simplest approximation of $W(u)$ was proposed as $W(u)=-0.5772-lnu$ for $u <$ 0.05. Other more exact approximations of the well function were summarized by R. Srivastava and A. Guzman-Guzman

Results and evaluation

The following figure compares the analytical solution, the result by OGS-5, and the result by OGS-6 (labeled as pressure) within the range that satisfies $u <$ 0.05.

The figure shows that there is a good match between the analytical solution and the numerical solution obtained by using OGS-5 or OGS-6.

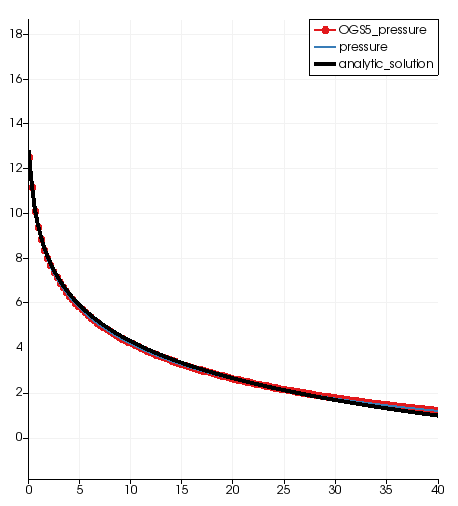
Some of the data of the above curves are given in the following table.

Comparison of solutions (where Distance means the distance from the position where the source term is applied).

Distance	Analytic	OGS-5	OGS-6	Error	Error
	Solution (ha)	(h5)	(h6)	($|\frac{h_5-h_a}{h_a}|$)	($|\frac{h_6-h_a}{h_a}|$)
0	12.8141	12.474	12.474	0.0265	0.0272
1.21799	8.9441	8.79341	8.79341	0.0168	0.0171
2.43597	7.48878	7.34717	7.34717	0.0189	0.0192
3.65396	6.59978	6.46176	6.46176	0.0209	0.0213
4.87195	5.94548	5.81072	5.81072	0.0226	0.0231
6.08994	5.43381	5.30267	5.30267	0.0241	0.0247
7.30792	5.00981	4.88283	4.88283	0.0253	0.0260
8.52591	4.65012	4.52793	4.52793	0.0262	0.0269
8.83041	4.56714	4.44623	4.44623	0.0264	0.0271
9.4394	4.4116	4.29344	4.29344	0.0267	0.0275
10.6574	4.12707	4.01501	4.01501	0.0271	0.0279
15.2248	3.28072	3.19698	3.19698	0.0255	0.0261
20.0968	2.61899	2.57517	2.57517	0.0167	0.0170
22.8373	2.31338	2.29626	2.29626	0.0074	0.0074
24.0553	2.18892	2.1846	2.1846	0.0019	0.0019
25.2732	2.07055	2.07958	2.07958	0.0043	0.0043
25.5777	2.04164	2.05407	2.05407	0.0060	0.0060
29.8407	1.67134	1.73518	1.73518	0.0381	0.0367

The analytical solutions are for an ideal problem with point wise pumping term. While for the FEM analysis, the point wise source value is distributed to the surface of a small hole around the source point in order to avoid the singularity. One can see from the table that the precisions of the FEM solutions are still acceptable with such transform of the point pumping term.