Simulate saturated single phase flow in fractured porous media: tests for inclined elements

There are four tests for the finite element analyses with inclined elements, which are the benchmarks to simulate the saturated single phase flow in fractured porous media. The correctness of the implementation of the inclined element approach is verified by the obtained flow, or flow velocity, orientation of these four benchmarks.

Flow in an inclined plane

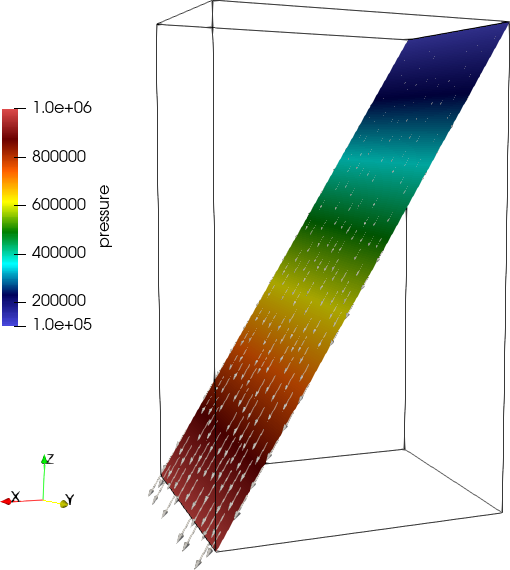
Under this topic, there are two benchmarks using the same 2D mesh on an inclined plane. The input files are given in the sub-directory of Inclined2DMesh, which includes one for hydro-steady state flow and another for transient flow under the fixed pressure difference on the top and the bottom boundary and the gravitational force. For the hydro-steady state one, it gives zero velocity. For the transient simulation, the orientation calculated velocity is shown in the following figure, which is parallel to the mesh plane as what expected.

Flow in rock matrix with two intersected fractures

The input files are given in the sub-directory of FractureIn3D. This benchmark tests the case of the mesh contains both 3D elements and inclined 2D element. The analysed domain has two intersected fractures. The brick shape domain is discretised into tetrahedra, while the two planes are discretised into triangles. The permeability of the continuous domain is

$$k_{xx}=1.0\cdot 10^{-18}, k_{yy}=3.0\cdot 10^{-18}, k_{xx}=3.0\cdot 10^{-18}\, \text{m}^2,$$

and the permeability of fractures are

$$ 10^{-14}\, \text{m}^2, \quad \text{and } 10^{-15}\, \text{m}^2,$$

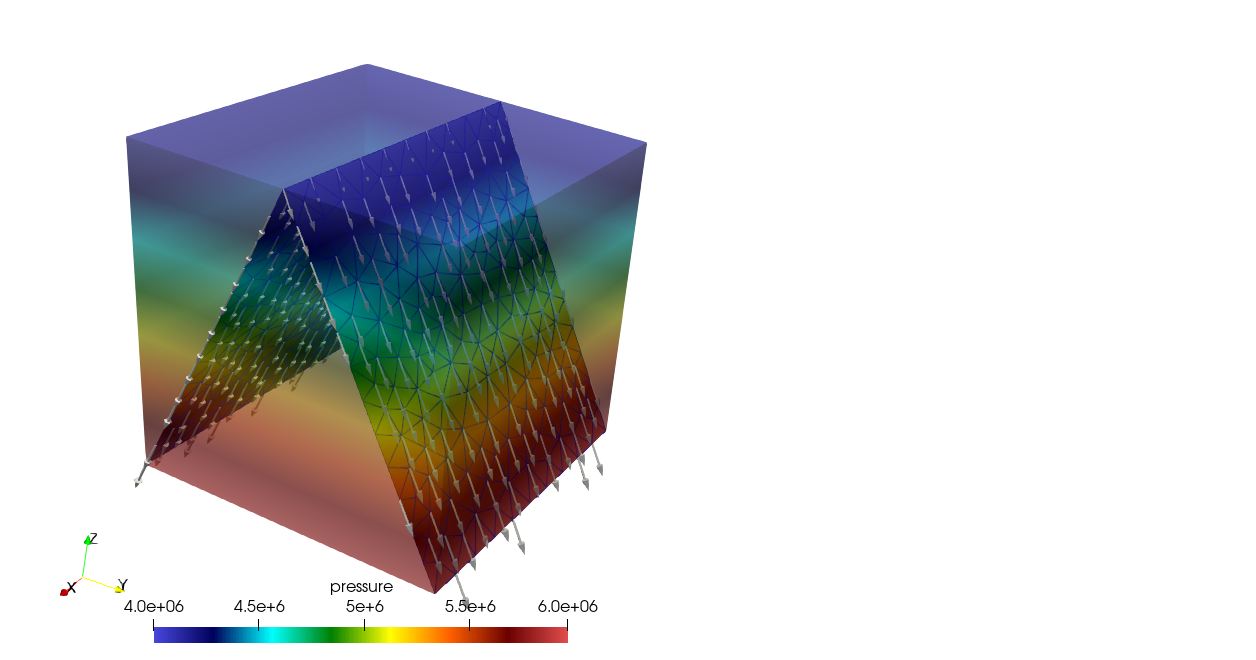
respectively. The flow is driven by the fixed pressure difference on the top and the bottom boundaries and the gravity. The following figure shows the pressure distribution and the flow orientation on the fractures. It can be seen that the flow orientation is exactly parallel to the fracture planes as what expected.

Line elements on a sphere

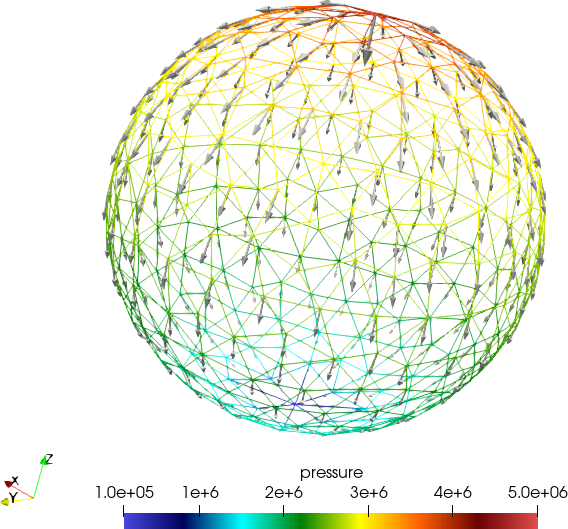
The input files are given in the sub-directory of 1Din3D. This an artificial example is used to test the simulation with a mesh only with inclined line elements. A sphere surface is used to discretise into triangle elements, and then all the edges of the elements are used as line elements of the mesh for this benchmark. That means all lines elements are on a sphere. A fixed pressure difference is applied at the two poles of the sphere. As shown in the following figure, the computed flow orientation is exactly on the tangent of the boundary of the vertical splices of the sphere.