Heatconduction (Dirichlet)

• Parabolic/T/1D_dirichlet/line_60_heat.prj

Equations

We consider homogeneous parabolic equation here:

$$ \begin{equation} \rho C_\textrm{p}\frac{\partial T}{\partial t} + \nabla\cdot(\lambda \nabla T) = 0 \quad \text{in }\Omega \end{equation}$$

w.r.t boundary conditions

$$ \eqalign{ T(x) = g_D(x) &\quad \text{on }\Gamma_D,\cr \lambda {\partial T(x) \over \partial n} = g_N(x) &\quad \text{on }\Gamma_N, } $$

where $T$ could be temperature, the subscripts $D$ and $N$ denote the Dirichlet- and Neumann-type boundary conditions, $n$ is the normal vector pointing outside of $\Omega$, and $\Gamma = \Gamma_D \cup \Gamma_N$ and $\Gamma_D \cap \Gamma_N = \emptyset$.

Problem specification and analytical solution

We solve the Parabolic equation on a line domain $[60\times 1]$ with $\lambda = 3.2$ and $\rho C_\textrm{p} = 2.5 \times 10^6$ w.r.t. the specific boundary conditions:

$$ \eqalign{ T(x) = 274.15 &\quad \text{on } (x=0) \subset \Gamma_D,\cr \lambda {\partial T(x) \over \partial n} = 0 &\quad \text{on } (x=60) \subset \Gamma_N. } $$

The solution of this problem is

$$ \begin{equation} T(x,t) = T_\textrm{b} \textrm{erfc}(\frac{x}{\sqrt{4\alpha t}}), \end{equation} $$

where $T_\textrm{b}$ is the boundary temperature, $\textrm{erfc}$ is the complementary error function and $\alpha = \lambda/(C_p \rho)$ is the thermal diffusivity.

Input files

The main project file is line_60_heat.prj. It describes the processes to be solved and the related process variables together with their initial and boundary conditions. It also references the mesh and geometrical objects defined on the mesh.

As of now a small portion of possible inputs is implemented; one can change:

• the mesh file
• the geometry file
• introduce more/different Dirichlet boundary conditions (different geometry or other constant values)
• introduce more/different Neumann boundary conditions (different geometry or other constant values)

The geometries used to specify the boundary conditions are given in the line_60_heat.gml file.

The input mesh line_60_heat.vtu is stored in the VTK file format and can be directly visualized in ParaView for example.

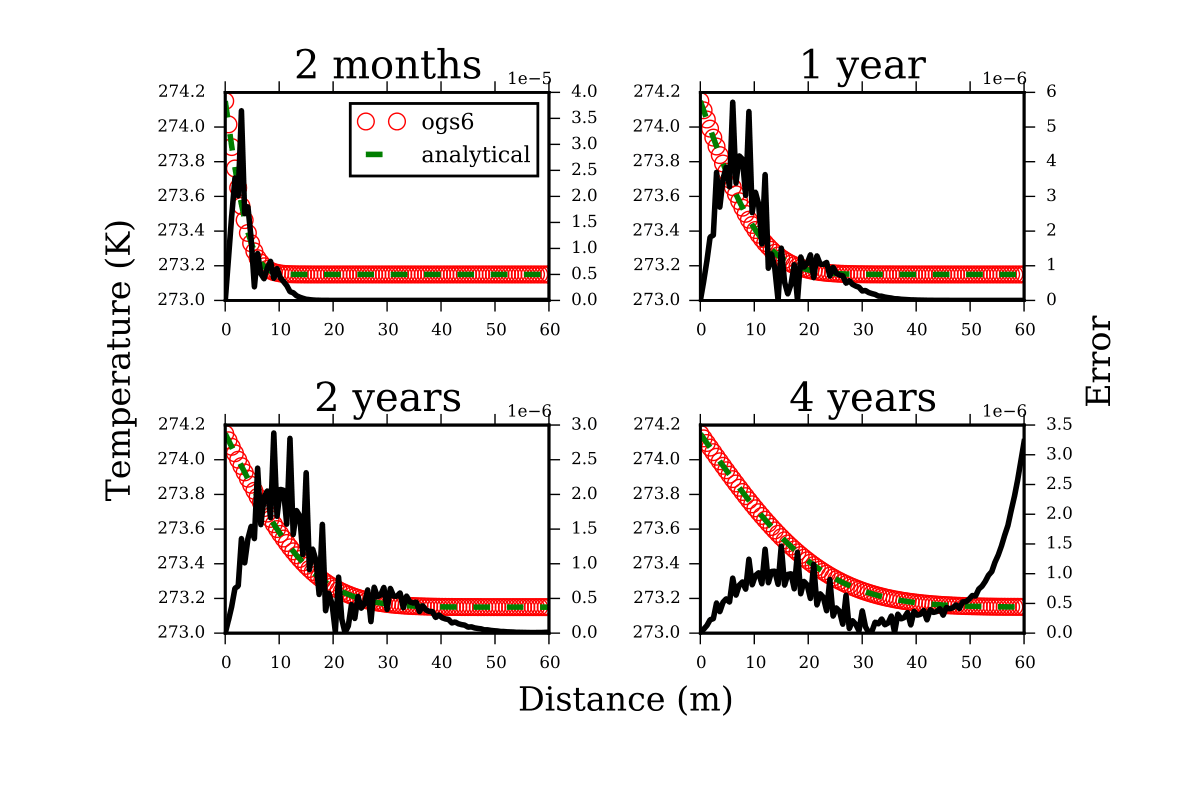
Results and evaluation

The result, written in the .vtu file, can be visualized with ParaView, for example.

Loading the line_60_heat_pcs_0_ts_65_t_5078125.000000.vtu file in ParaView and Plotting over line. Compared to the analytical solution temperature_analytical.vtu, the results are very good: