BHE with groundwater advection
Problem description
When groundwater flow is present, advective heat transport in the soil matrix has to be considered. Hence, the governing equation for advective and conductive heat transport in an isotropic porous media can be expressed (in 2D form) as follows:
$$ \begin{equation} \rho c \frac{\partial T}{\partial t} + \rho_wc_w \left(u_x\frac{\partial T}{\partial x} + u_y\frac{\partial T}{\partial y}\right) - \lambda \left(\frac{\partial^2 T}{\partial x^2}+\frac{\partial^2 T}{\partial y^2}\right) = 0 \end{equation} $$where $u$$=(u_x,u_y)$ denotes the Darcy velocity. For simplification, we assume that $u$ is uniform and in the $x$ direction, i.e. $u_y=0$. In addition, the porous medium is assumed to be infinite with homogeneous initial temperature as well as hydraulic/thermal parameters. Under these assumptions, the analytical solution for the ground temperature response to a constant and uniform line source located at (0, 0) with infinite length along the $z$ direction is expressed as (Diao et al. (2004)):
$$ \begin{equation} \Delta T(x,y,t)=\frac{q_L}{4\pi\lambda}{\rm exp}\left[\frac{v_Tx}{2a}\right]\int_{0}^{v_T^2t/4a} \frac{1}{\psi}{\rm exp}\left[-\psi-\frac{v_T^2(x^2+y^2)}{16a^2\psi}\right] {\rm d}\psi \end{equation} $$in which $v_T=u_x\rho_w c_w/\rho c$ is the effective heat transport velocity (Molina-Giraldo et al. (2011)) and $q_L$ is the continuous heat exchange rate per unit length. As a common practice, the BHE can be approximated by a line source (e.g. Eskilson (1987) and Diao et al. (2004)). In cases where the BHE penetrates the entire depth of the 3D porous medium, the above analytical solution can be applied to solve the spatio-temporal distribution of the induced ground temperature.
Model Setup
The input files for the full simulation including the analytical solution for the soil temperature can be found here. The geometry of the model is illustrated in Figure 1. The depth of the model domain is 15 m with an areal extent of 80 m x 80 m. The BHE is 1U-type and is represented by a straight line located at $x=0$ m and $y=30$ m. In this benchmark the groundwater flow is set in the $y$ direction. Accordingly, the mesh was intentionally extended downstream of the BHE, so that the boundary effects on the ground temperature distribution can be neglected even for the long-term simulation. Detailed parameters for the soil heat transport model can be found in the following table.
| Parameter | Symbol | Value | Unit |
|---|---|---|---|
| Thermal conductivity of the porous medium | $\lambda$ | 2.5 | $\mathrm{W m^{-1} K^{-1}}$ |
| Volumetric heat capacity of the porous medium | $\rho c$ | $2.818\times10^{6}$ | $\mathrm{Jm^{-3}K^{-1}}$ |
| Length of the BHE | $L$ | 15 | $\mathrm{m}$ |
| Darcy velocity | $u_y$ | $1\times10^{-7}$ | $\mathrm{m s^{-1}}$ |
| Specific heat exchange rate of the BHE | $q_L$ | 20 | $\mathrm{W m^{-1}}$ |
| Initial ground temperature | $T_{ini}$ | 25 | $^{\circ}$C |
The BHE parameters are only relevant for the numerical model and are adopted from the 3D Beier sandbox benchmark.
Geometry and mesh of the BHE model
Results
In Figure 2, the numerically simulated ground temperature distribution from OGS-6 is shown for the $z=-7$ m plane after $t=2$ years. Also, the result is compared with the moving line source analytical solution (evaluated using MATLAB®) in Figure 3. The comparison demonstrates that the numerical results and analytical solution match very well as the maximum relative error of ground temperature is less than 0.2 %. The largest difference is found near the BHE node towards which the analytical solution approaches infinity.
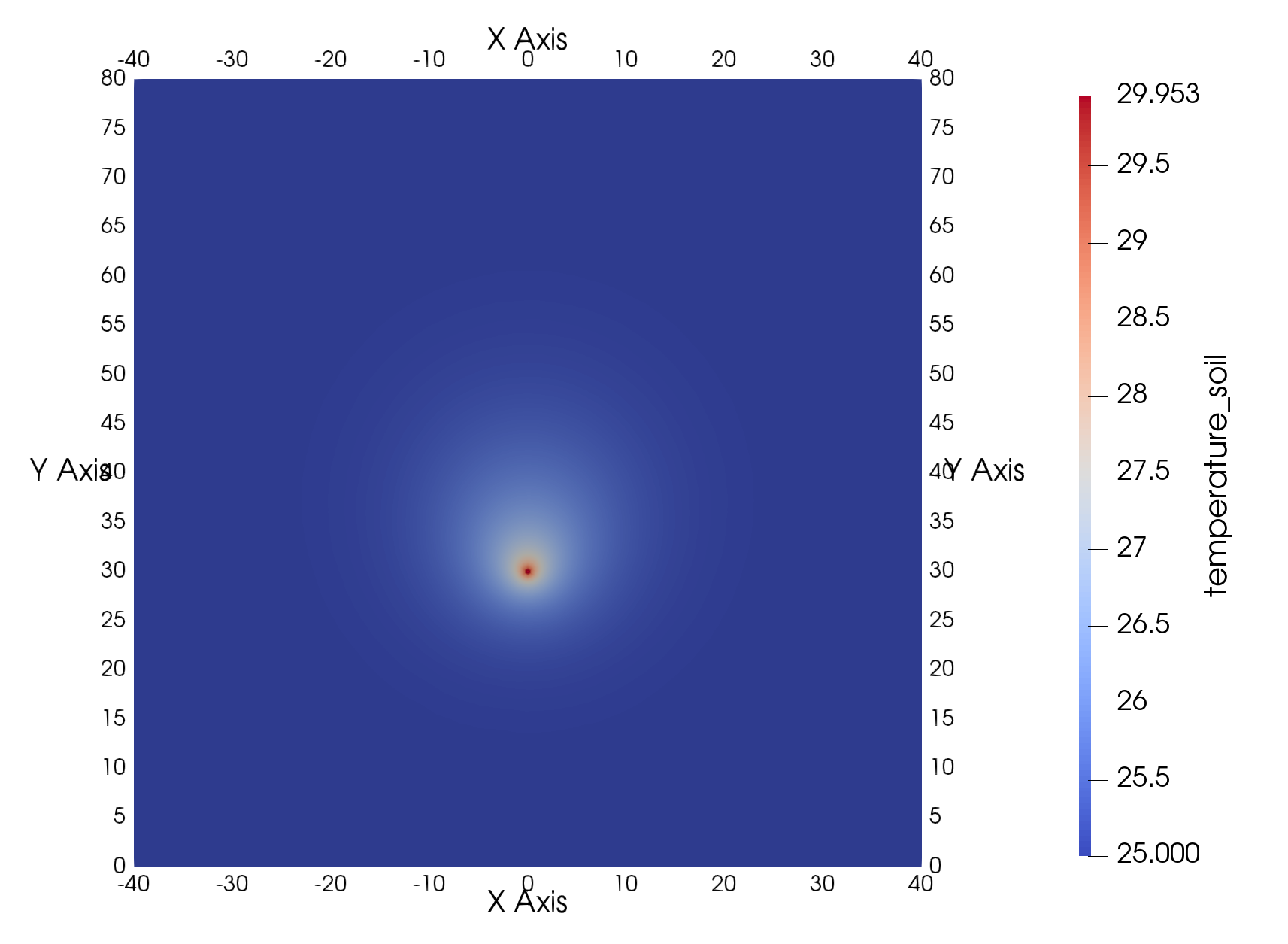
Ground temperature distribution after two years at $z=-7$ m.
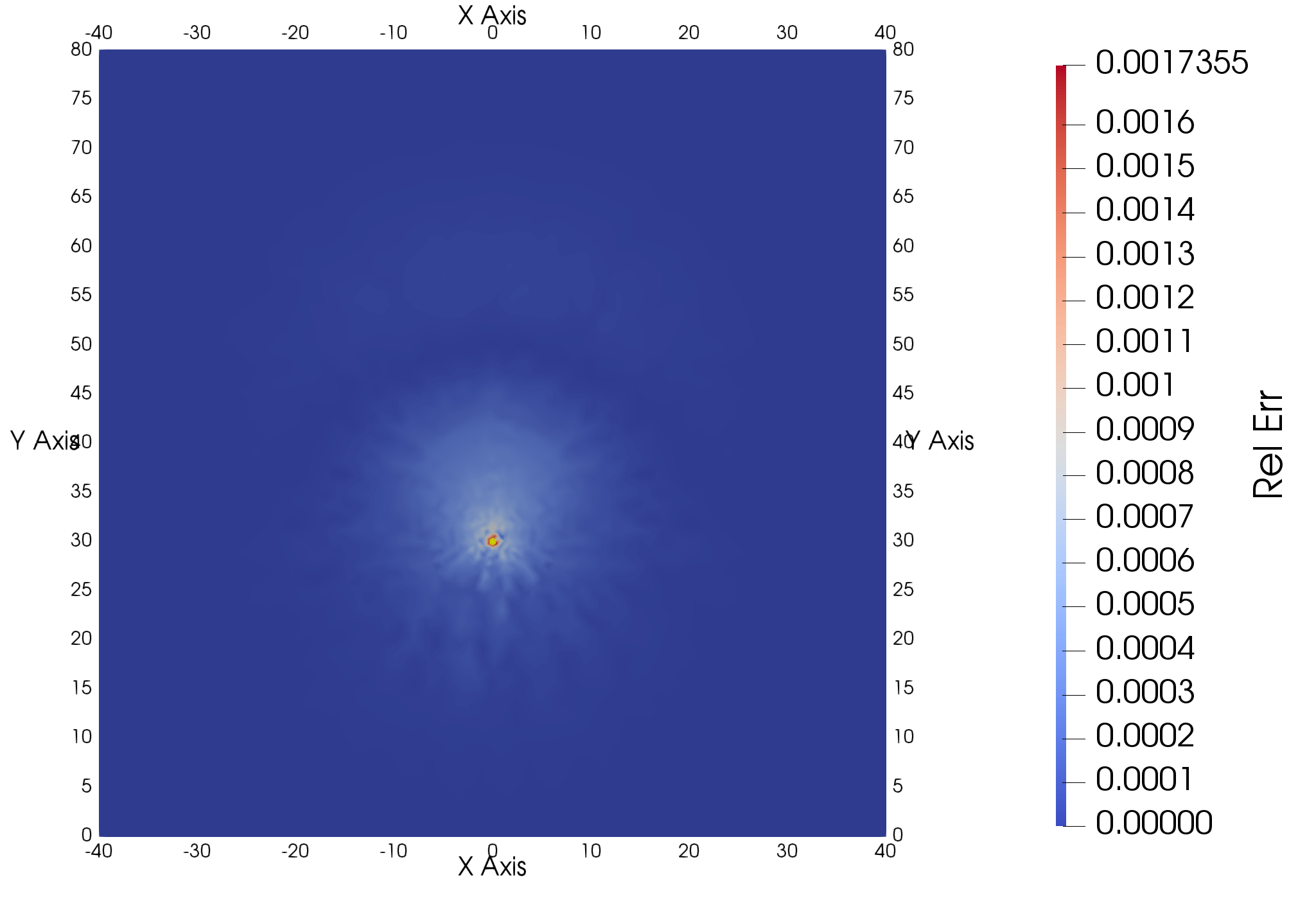
Comparison of OGS-6 results and analytical solution. Note the singularity of the analytical solution at the BHE node.
References
[1] Diao, N., Li, Q., & Fang, Z. (2004). Heat transfer in ground heat exchangers with groundwater advection. International Journal of Thermal Sciences, 43(12), 1203-1211.
[2] Molina-Giraldo, N., Blum, P., Zhu, K., Bayer, P., & Fang, Z. (2011). A moving finite line source model to simulate borehole heat exchangers with groundwater advection. International Journal of Thermal Sciences, 50(12), 2506-2513.
[3] P. Eskilson, Thermal analysis of heat extraction boreholes, Ph.D. Thesis, University of Lund, Lund, Sweden, 1987.
This article was written by Boyan Meng, Chaofan Chen, Haibing Shao. If you are missing something or you find an error please let us know.
Generated with Hugo 0.122.0
in CI job 449919
|
Last revision: April 23, 2024
Commit: [PL/LD] Use generic cell average output 3557e29
| Edit this page on