Benchmark of 3D Beier sandbox
Problem description
The U-type Borehole Heat Exchanger (BHE) is always utilized to extract the shallow geothermal energy all over the world. In this benchmark, the 1-U type BHE numerical model in OGS-6 was verified through comparing with experimental results obtained by Beier et al. (2011). In their experiment, one single U-type BHE was embedded in a sandbox together with some temperature sensors at the specific locations in the sand. Using the pump to circulate the fluid in the U-type pipe, which was heated by a electrical heater. Different from the geothermal energy exploitation, the temperature of the sand will be lifted due to the inflow temperature of BHE is higher than its outflow temperature, which was dynamically monitored as one of the key results in the Thermal Response Test (TRT).
Model Setup
The numerical model was established using dual continuum method Diersch et al. (2011), in which the BHE is represented by the line element and 3D prism stands for the sand part. The numerical geometry model can be visualized as shown in Figure 1. Thus, there are two material groups in the model distinguishing the soil part and the BHE part. The length of the whole box is 18.5 m with a square cross section of 5 m per side to avoid the impact of boundary conditions on the soil temperature. Detailed parameters for the model configuration are listed in the following table.
| Parameter | Symbol | Value | Unit |
|---|---|---|---|
| Soil thermal conductivity | $\lambda_{s}$ | 2.78 | $\mathrm{W m^{-1} K^{-1}}$ |
| Soil heat capacity | $(\rho c)_{soil}$ | $3.2\times10^{6}$ | $\mathrm{Jm^{-3}K^{-1}}$ |
| Length of the BHE | $L$ | 18 | $\mathrm{m}$ |
| Diameter of the BHE | $D$ | 13 | $\mathrm{cm}$ |
| Diameter of the pipeline | $d$ | 2.733 | $\mathrm{cm}$ |
| Wall thickness of the pipeline | $b$ | 0.3035 | $\mathrm{cm}$ |
| Distance between pipelines | $w$ | 5.3 | $\mathrm{cm}$ |
| Pipeline wall thermal conductivity | $\lambda_{p}$ | 0.39 | $\mathrm{W m^{-1} K^{-1}}$ |
| Grout thermal conductivity | $\lambda_{g}$ | 0.806 | $\mathrm{W m^{-1} K^{-1}}$ |
| Grout heat capacity | $(\rho c)_{grout}$ | $3.8\times10^{6}$ | $\mathrm{Jm^{-3}K^{-1}}$ |

Sandbox model
In Beier’s experiment, the inner diameter of aluminum pipe is 12.6 $\mathrm{cm}$ and the borehole wall thickness of aluminum is 0.2 $\mathrm{cm}$. In the numerical model, the borehole wall feature cannot be reflected because of the line elements. Therefore, the diameter of the BHE in numerical model was set 13 $\mathrm{cm}$. Meanwhile, the grout’s thermal conductivity was increased from original 0.73 $\mathrm{W m^{-1} K^{-1}}$ to 0.806 $\mathrm{W m^{-1} K^{-1}}$. As for the circulating water in the BHE pipe, the thermal physical parameters are taken from the state at an average temperature of approx. 309.15 K.
OGS-6 Input Files
The detailed input file can be seen from the .prj file. The inflow temperature of the BHE, which was imposed as boundary condition of the BHE can be shown in Figure 2. Initial conditions of inflow and outflow temperature for the BHE were directly obtained from the measurements at t=0. For the initial soil temperature, the average value of all sensors placed in the sand and the borehole wall was set in the numerical model.
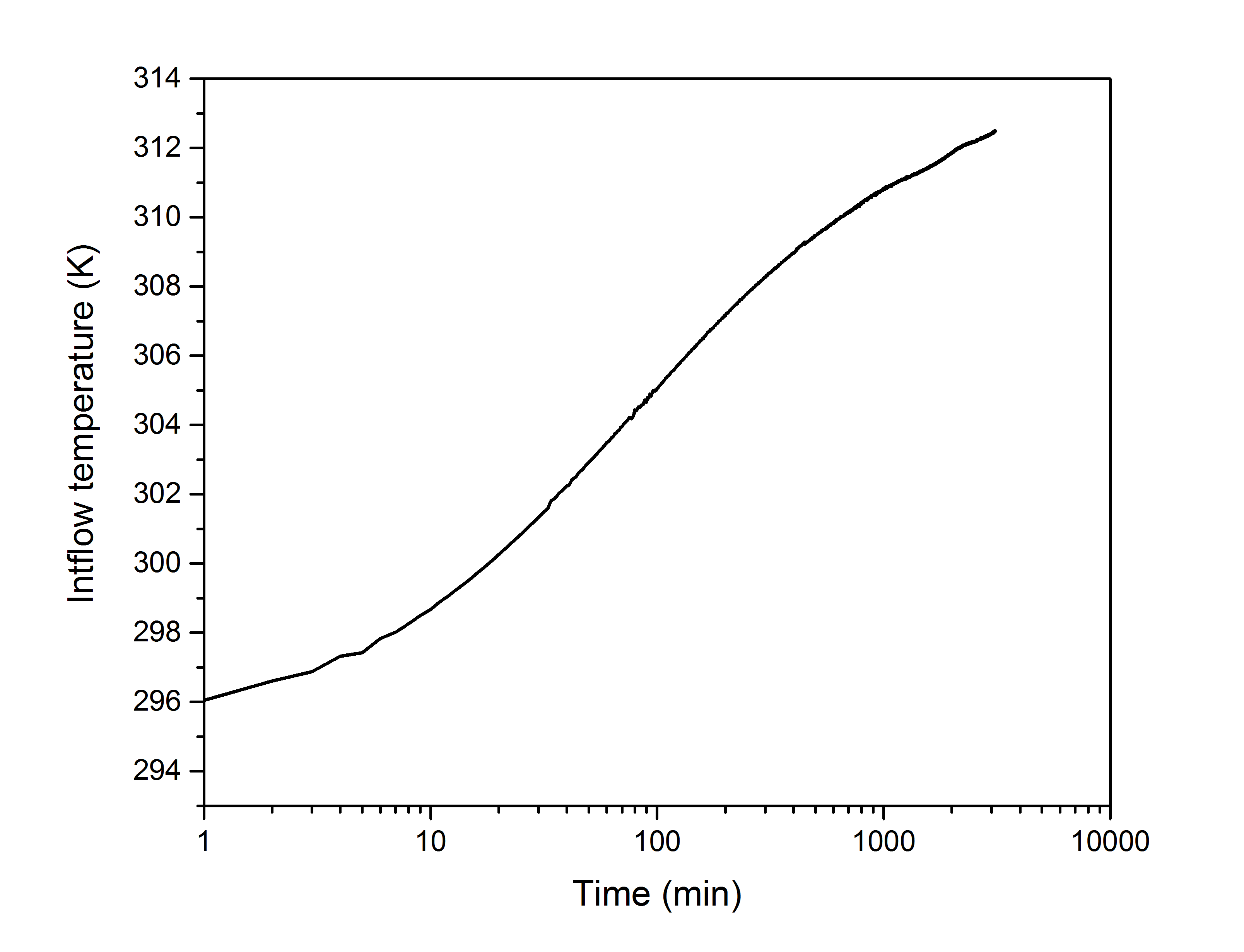
Inflow temperature curve as the BHE boundary condition
Results
The numerical outflow temperature of OGS-5 (Shao et al. (2016)) and OGS-6 was compared with the experimental results, which is presented in the Figure 3. And the soil temperature at different locations among experimental and numerical results were compared and shown in the Figure 4. The comparison figures demonstrate that the numerical results and experimental data can fit very well and the largest relative error is 0.17% on the wall temperature and 0.014% on the outflow temperature. The initial temperature of borehole wall in numerical model was set an average value as mentioned in the above, which has initial error of 0.07 K compared to the experimental data. Besides, normally, the error of measuring temperatures during experiment, difference on the real thermal physical parameters of the sand and the BHE are all at the same value range. Therefore, it can be concluded that the numerical model of 1U-type BHE is fully verified.
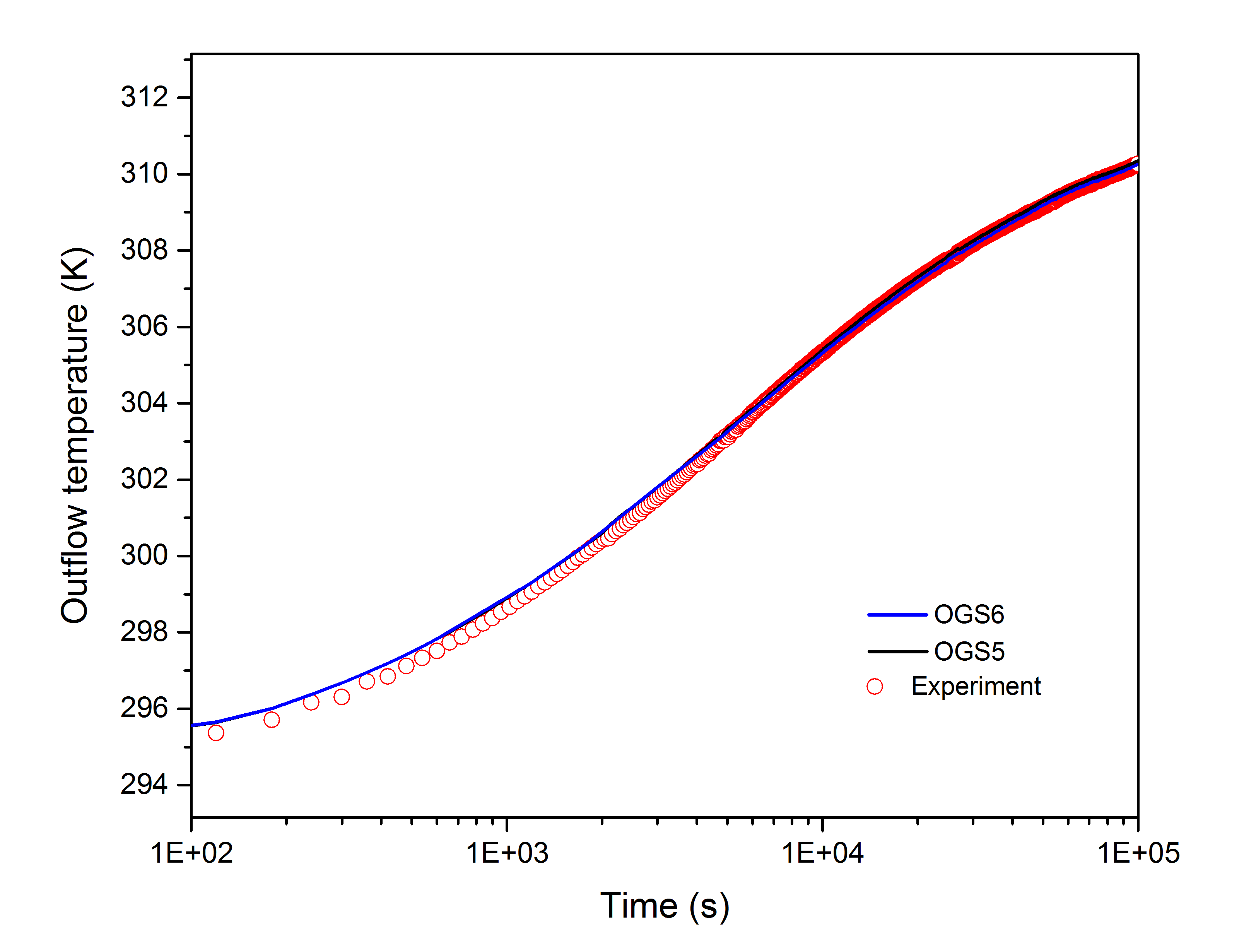
Comparison with experiment and OGS-5 results regarding outflow temperature of the BHE
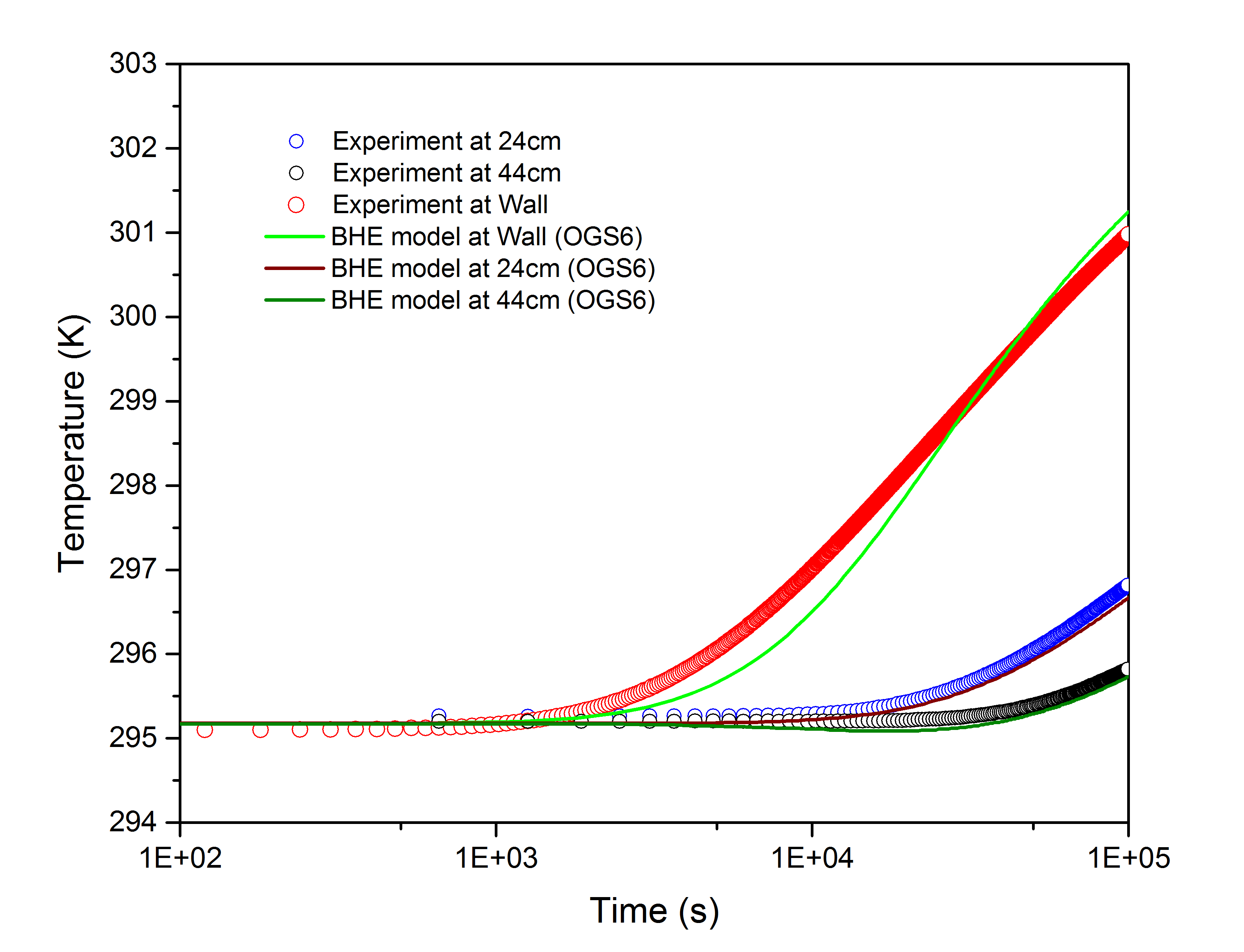
Comparison of modelled and measured wall and soil temperatures
References
[1] Richard A Beier, Marvin D Smith, and Jeffrey D Spitler. Reference data setsfor vertical borehole ground heat exchanger models and thermal responsetest analysis. Geothermics, 40(1):79–85, 2011
[2] Diersch, H. J., Bauer, D., Heidemann, W., Rühaak, W., & Schätzl, P. (2011). Finite element modeling of borehole heat exchanger systems: Part 1. Fundamentals. Computers & Geosciences, 37(8), 1122-1135.
[3] Haibing Shao, Philipp Hein, Agnes Sachse, and Olaf Kolditz. GeoenergyModeling II: Shallow Geothermal Systems. Springer, 2016
This article was written by Chaofan Chen, Philipp Hein, Haibing Shao. If you are missing something or you find an error please let us know.
Generated with Hugo 0.122.0
in CI job 449919
|
Last revision: April 23, 2024
Commit: [PL/LD] Use generic cell average output 3557e29
| Edit this page on