OpenGeoSys

Hydraulic Fracturing in the Toughness-Dominated Regime

This page is based on a Jupyter notebook.

Hydraulic Fracturing in the Toughness-Dominated Regime

Under the toughness-dominated regime without leak-off, the fluid viscosity dissipation is negligible compared to the energy released for fracture surface formation (Detournay et al., 2016). Therefore, in this regime, we can neglect the pressure loss within the fracture and use the Sneddon solution for crack opening (Bourdin et al., 2012, Sneddon et al., 1969) to determine the pressure and length evolution.

The work of the pressure force is as follows:

$$ \begin{equation} \mathcal{W}(R) =\frac{2 p^2 a^2}{E'}. \end{equation} $$

Applying Clapeyron’s theorem, the elastic energy can be determined as

$$ \begin{equation} \mathcal{E}(R) =-\frac{\pi p^2 a^2}{E'}, \end{equation} $$

and the energy release rate with respect to the crack length $a$ propagating along the initial inclination is

$$ \begin{equation} G(R) = - \frac{\partial \mathcal{E}}{\partial (2 a)} = \frac{\pi p^2 a}{E'}. \end{equation} $$

Griffith's criterion (Griffith et al., 1920) states that the fracture propagates when $G=G_c$ and the critical volume for crack propagation is $V_c := \sqrt{\dfrac{4 \pi G_c a^3}{E' }}$ in a quasi-static volume control setting (the fracture propagation is always unstable with pressure control).

The evolution of the corresponding pressure and fracture length

$$ \begin{equation} p(V) = \begin{cases} \dfrac{E' V}{2 \pi a_0^2} &\text{for} V < V_c \\ \left[ \dfrac{2 E' G_c^2}{\pi V} \right] ^{\frac{1}{3}}&\text{for} V \geq V_c, \end{cases} \end{equation} $$ $$ \begin{equation} a(V) = \begin{cases} a_0 & V < V_c \\ \left[ \dfrac{E' V^2}{4 \pi G_c} \right ] ^{\frac{1}{3}} & V \geq V_c. \end{cases} \end{equation} $$

Problem Description

Based on Sneddon's solution (Sneddon et al., 1969), we verified the model with plane-strain hydraulic fracture propagation in a toughness-dominated regime. In an infinite 2D domain, the problem was solved with a line fracture $[-a_0, a_0] \times \{0\}$ ($a_0$ = 0.05). We considered a large finite domain $[-40a_0,40a_0] \times [-40a_0,40a_0]$ to account for the infinite boundaries in the closed-form solution. The effective size of an element, $h$, is $1\times10^{-2}$.

Schematic view of hydraulic fracturing problem and Boundary conditions
Schematic view of hydraulic fracturing problem and Boundary conditions.

  • In order to have the hydraulic fracturing in the toughness dominated-regime, add, $\texttt{propagating}$ in the project file.
  • Yoshioka et al., 2019 provides additional information on the implementation, use of real material properties, and rescaling of the phase-field energy functional.

Input Data

Taking advantage of the linearity of the system, the simulations were run with the dimensionless properties listed in the Table below.

Name Value Symbol
Young’s modulus 1 $E$
Poisson’s ratio 0.15 $\nu$
Fracture toughness 1 $G_{c}$
Regularization parameter 2$h$ $\ell_s$
Length 4 $L$
Height 4 $H$
Initial crack length 0.1 $2a_0$ 
import argparse
import math
import os
import re
import time

import gmsh
import matplotlib.pyplot as plt
import numpy as np
from ogs6py import ogs
from ogstools.msh2vtu import run

pi = math.pi
plt.rcParams["text.usetex"] = True
E = 1.0
nu = 0.15
Gc = 1.0
h = 0.01
a0 = 0.05  # half of the initial crack length

phasefield_model = "AT1"  # AT1/AT2

Output Directory and Project File

# file's name
prj_name = "Kregime_Propagating.prj"
meshname = "mesh_full_pf"

from pathlib import Path

out_dir = Path(os.environ.get("OGS_TESTRUNNER_OUT_DIR", "_out"))
if not out_dir.exists():
    out_dir.mkdir(parents=True)

Mesh Generation

def mesh_generation(lc, lc_fine):
    """
    lc ... characteristic length for coarse meshing
    lc_fine ... characteristic length for fine meshing
    """
    L = 4.0  # Length
    H = 4.0  # Height
    b = 0.4  # Length/Height of subdomain with fine mesh

    # Before using any functions in the Python API, Gmsh must be initialized
    gmsh.initialize()
    gmsh.option.setNumber("General.Terminal", 1)
    gmsh.model.add("rectangle")

    # Dimensions
    dim0 = 0
    dim1 = 1
    dim2 = 2

    # Points
    gmsh.model.geo.addPoint(-L / 2, -H / 2, 0, lc, 1)
    gmsh.model.geo.addPoint(L / 2, -H / 2, 0, lc, 2)
    gmsh.model.geo.addPoint(L / 2, H / 2, 0, lc, 3)
    gmsh.model.geo.addPoint(-L / 2, H / 2, 0, lc, 4)
    gmsh.model.geo.addPoint(-b, -b - lc_fine / 2, 0, lc_fine, 5)
    gmsh.model.geo.addPoint(b, -b - lc_fine / 2, 0, lc_fine, 6)
    gmsh.model.geo.addPoint(b, b + lc_fine / 2, 0, lc_fine, 7)
    gmsh.model.geo.addPoint(-b, b + lc_fine / 2, 0, lc_fine, 8)

    # Lines
    gmsh.model.geo.addLine(1, 2, 1)
    gmsh.model.geo.addLine(2, 3, 2)
    gmsh.model.geo.addLine(3, 4, 3)
    gmsh.model.geo.addLine(4, 1, 4)
    gmsh.model.geo.addLine(5, 6, 5)
    gmsh.model.geo.addLine(6, 7, 6)
    gmsh.model.geo.addLine(7, 8, 7)
    gmsh.model.geo.addLine(8, 5, 8)

    # Line loops
    gmsh.model.geo.addCurveLoop([1, 2, 3, 4], 1)
    gmsh.model.geo.addCurveLoop([5, 6, 7, 8], 2)

    # Add plane surfaces defined by one or more curve loops.
    gmsh.model.geo.addPlaneSurface([1, 2], 1)
    gmsh.model.geo.addPlaneSurface([2], 2)

    gmsh.model.geo.synchronize()

    # Prepare structured grid
    gmsh.model.geo.mesh.setTransfiniteCurve(
        6, math.ceil(2 * b / lc_fine + 2), "Progression", 1
    )
    gmsh.model.geo.mesh.setTransfiniteCurve(
        8, math.ceil(2 * b / lc_fine + 2), "Progression", 1
    )
    gmsh.model.geo.mesh.setTransfiniteSurface(2, "Alternate")

    gmsh.model.geo.mesh.setRecombine(dim2, 1)
    gmsh.model.geo.mesh.setRecombine(dim2, 2)

    gmsh.model.geo.synchronize()

    # Physical groups
    P1 = gmsh.model.addPhysicalGroup(dim0, [1])
    gmsh.model.setPhysicalName(dim0, P1, "P1")

    P2 = gmsh.model.addPhysicalGroup(dim0, [2])
    gmsh.model.setPhysicalName(dim0, P2, "P2")

    Bottom = gmsh.model.addPhysicalGroup(dim1, [1])
    gmsh.model.setPhysicalName(dim1, Bottom, "Bottom")

    Right = gmsh.model.addPhysicalGroup(dim1, [2])
    gmsh.model.setPhysicalName(dim1, Right, "Right")

    Top = gmsh.model.addPhysicalGroup(dim1, [3])
    gmsh.model.setPhysicalName(dim1, Top, "Top")

    Left = gmsh.model.addPhysicalGroup(dim1, [4])
    gmsh.model.setPhysicalName(dim1, Left, "Left")

    Computational_domain = gmsh.model.addPhysicalGroup(dim2, [1, 2])
    gmsh.model.setPhysicalName(dim2, Computational_domain, "Computational_domain")
    gmsh.model.geo.synchronize()

    output_file = f"{out_dir}/" + meshname + ".msh"
    gmsh.model.mesh.generate(dim2)
    gmsh.write(output_file)
    gmsh.finalize()

Pre-Processing

def pre_processing(h, a0):
    mesh = pv.read(f"{out_dir}/mesh_full_pf_domain.vtu")
    phase_field = np.ones((len(mesh.points), 1))
    pv.set_plot_theme("document")

    for node_id, x in enumerate(mesh.points):
        if (
            (mesh.center[0] - x[0]) <= a0 + 0.001 * h
            and (mesh.center[0] - x[0]) >= -a0 - 0.001 * h
            and (mesh.center[1] - x[1]) < h / 2 + 0.001 * h
            and (mesh.center[1] - x[1]) > -h / 2 - 0.001 * h
        ):
            phase_field[node_id] = 0.0

    mesh.point_data["phase-field"] = phase_field
    mesh.save(f"{out_dir}/mesh_full_pf_OGS_pf_ic.vtu")

Run the Simulation

import pyvista as pv

pv.set_plot_theme("document")
if "PYVISTA_HEADLESS" in os.environ:
    pv.start_xvfb()
pv.set_jupyter_backend("static")


def Hydraulic_Fracturing_Toughness_Dominated_numerical(h, phasefield_model):
    # mesh properties
    ls = 2 * h
    # generate prefix from properties
    filename = f"results_h_{h:0.4f}_{phasefield_model}"
    mesh_generation(0.1, h)
    # Convert GMSH (.msh) meshes to VTU meshes appropriate for OGS simulation.
    input_file = f"{out_dir}/" + meshname + ".msh"
    args = argparse.Namespace(
        filename=input_file,
        output=f"{out_dir}/" + meshname,
        dim=0,
        delz=False,
        swapxy=False,
        rdcd=True,
        ogs=True,
        ascii=False,
    )
    run(args)

    # As a preprocessing step, define the initial phase-field (crack).
    pre_processing(h, a0)
    # change properties in prj file #For more information visit: https://github.com/joergbuchwald/ogs6py
    model = ogs.OGS(
        INPUT_FILE=prj_name,
        PROJECT_FILE=f"{out_dir}/{prj_name}",
        MKL=True,
        args=f"-o {out_dir}",
    )
    model.replace_parameter_value(name="ls", value=ls)
    model.replace_text(phasefield_model, xpath="./processes/process/phasefield_model")
    model.replace_text(filename, xpath="./time_loop/output/prefix")
    model.write_input()
    # run simulation with ogs
    t0 = time.time()
    print(">>> OGS started execution ... <<<")
    ! ogs {out_dir}/{prj_name} -o {out_dir} > {out_dir}/log.txt
    tf = time.time()
    print(">>> OGS terminated execution  <<< Elapsed time: ", round(tf - t0, 2), " s.")
Hydraulic_Fracturing_Toughness_Dominated_numerical(h, phasefield_model)
Info    : Meshing 1D...
Info    : [  0%] Meshing curve 1 (Line)
Info    : [ 20%] Meshing curve 2 (Line)
Info    : [ 30%] Meshing curve 3 (Line)
Info    : [ 40%] Meshing curve 4 (Line)
Info    : [ 50%] Meshing curve 5 (Line)
Info    : [ 70%] Meshing curve 6 (Line)
Info    : [ 80%] Meshing curve 7 (Line)
Info    : [ 90%] Meshing curve 8 (Line)
Info    : Done meshing 1D (Wall 0.000457345s, CPU 0.000696s)
Info    : Meshing 2D...
Info    : [  0%] Meshing surface 1 (Plane, Frontal-Delaunay)
Info    : [  0%] Blossom: 24032 internal 482 closed
Info    : [  0%] Blossom recombination completed (Wall 0.311675s, CPU 0.311437s): 7878 quads, 0 triangles, 0 invalid quads, 0 quads with Q < 0.1, avg Q = 0.793024, min Q = 0.371315
Info    : [ 50%] Meshing surface 2 (Transfinite)
Info    : Done meshing 2D (Wall 0.461565s, CPU 0.461475s)
Info    : 14439 nodes 14848 elements
Info    : Writing '/var/lib/gitlab-runner/builds/vZ6vnZiU/1/ogs/build/release-petsc/Tests/Data/PhaseField/Kregime_Propagating_jupyter_notebook/Kregime_Propagating_jupyter/mesh_full_pf.msh'...
Info    : Done writing '/var/lib/gitlab-runner/builds/vZ6vnZiU/1/ogs/build/release-petsc/Tests/Data/PhaseField/Kregime_Propagating_jupyter_notebook/Kregime_Propagating_jupyter/mesh_full_pf.msh'
Output: /var/lib/gitlab-runner/builds/vZ6vnZiU/1/ogs/build/release-petsc/Tests/Data/PhaseField/Kregime_Propagating_jupyter_notebook/Kregime_Propagating_jupyter/mesh_full_pf

Original mesh (read)
14439 points in 3 dimensions; cells: 2 vertex, 160 line, 14358 quad; point_data=['gmsh:dim_tags']; cell_data=['gmsh:physical', 'gmsh:geometrical']; cell_sets=['P1', 'P2', 'Bottom', 'Right', 'Top', 'Left', 'Computational_domain', 'gmsh:bounding_entities']
##
Detected mesh dimension: 2
##
Domain mesh (written)
14439 points in 3 dimensions; cells: 14358 quad; point_data=['original_node_number']; cell_data=['MaterialIDs']; cell_sets=[]
##
Boundary mesh (written)
160 points in 3 dimensions; cells: 160 line; point_data=['bulk_node_ids']; cell_data=['bulk_elem_ids']; cell_sets=[]
##
Submesh P1 (written)
1 points in 3 dimensions; cells: 1 vertex; point_data=['bulk_node_ids']; cell_data=['gmsh:physical']; cell_sets=[]
##
Submesh P2 (written)
1 points in 3 dimensions; cells: 1 vertex; point_data=['bulk_node_ids']; cell_data=['gmsh:physical']; cell_sets=[]
##
Submesh Bottom (written)
41 points in 3 dimensions; cells: 40 line; point_data=['bulk_node_ids']; cell_data=['bulk_elem_ids']; cell_sets=[]
##
Submesh Right (written)
41 points in 3 dimensions; cells: 40 line; point_data=['bulk_node_ids']; cell_data=['bulk_elem_ids']; cell_sets=[]
##
Submesh Top (written)
41 points in 3 dimensions; cells: 40 line; point_data=['bulk_node_ids']; cell_data=['bulk_elem_ids']; cell_sets=[]
##
Submesh Left (written)
41 points in 3 dimensions; cells: 40 line; point_data=['bulk_node_ids']; cell_data=['bulk_elem_ids']; cell_sets=[]
##
Submesh Computational_domain (written)
14439 points in 3 dimensions; cells: 14358 quad; point_data=['bulk_node_ids']; cell_data=['MaterialIDs']; cell_sets=[]
##
>>> OGS started execution ... <<<
>>> OGS terminated execution  <<< Elapsed time:  259.22  s.

Post-Processing

Analytical Solution for the Evolution of Fracture Length and Pressure

def Analytical_solution(phasefield_model, h):
    v = np.linspace(1e-10, 0.3, 31)
    pres = np.linspace(0, 1.0, 31)
    length = np.linspace(0, 1.0, 31)

    ls = 2 * h

    # Effective Gc and a for AT1/A2
    if phasefield_model == "AT1":
        Gc_ref = Gc * (3 * h / 8.0 / ls + 1.0)
        a_eff = a0 * (1 + pi * ls / (4.0 * a0 * (3 * h / 8.0 / ls + 1.0)))
    elif phasefield_model == "AT2":
        Gc_ref = Gc * (h / (2.0 * ls) + 1.0)
        a_eff = a0 * (1 + pi * ls / (4.0 * a0 * (h / (2.0 * ls) + 1.0)))

    Eprime = E / (1 - nu**2)

    V_c = (4 * pi * Gc_ref * a_eff**3 / Eprime) ** 0.5
    P_c = (Eprime * Gc_ref / (pi * a_eff)) ** 0.5

    for i in range(len(v)):
        if v[i] < V_c:
            pres[i] = Eprime * v[i] / (2 * pi * a_eff**2) / P_c
            length[i] = a_eff
        else:
            pres[i] = (2 * Eprime * Gc_ref**2 / (pi * v[i])) ** 0.333333 / P_c
            length[i] = (Eprime * v[i] ** 2 / (4 * pi * Gc_ref)) ** 0.333333

    return v, pres, length, Gc_ref, P_c


fluidVolume_analytical = Analytical_solution(phasefield_model, h)[0]
pressure_analytical = Analytical_solution(phasefield_model, h)[1]
length_analytical = Analytical_solution(phasefield_model, h)[2]
Gc_ref = Analytical_solution(phasefield_model, h)[3]
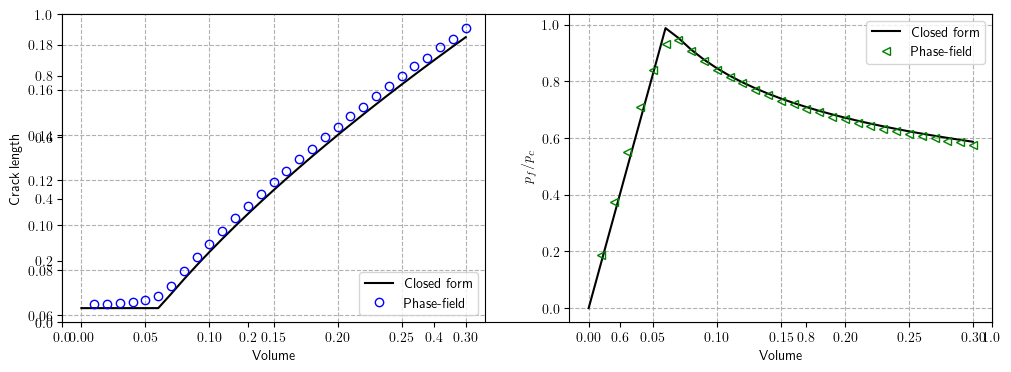
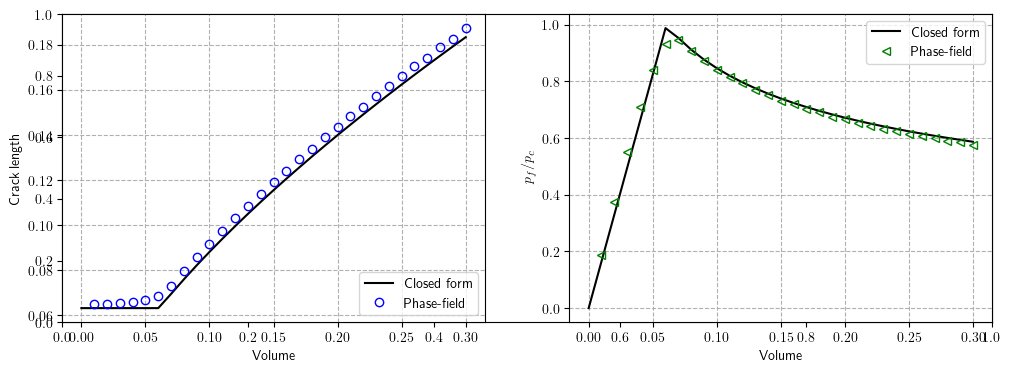
P_c = Analytical_solution(phasefield_model, h)[4]

Phase Field Versus Analytical Solution for Fracture Length and Pressure Evolution

In phase field approach, we can retrieve the crack length $a$ as:

$$ \begin{equation} a = \dfrac{\displaystyle \int_\Omega \frac{G_c}{4 c_n} \left(\frac{(1-v)^n}{\ell}+ \ell |\nabla v|^2\right)\,\mathrm{d} \Omega }{G_c \left( \dfrac{h}{4 c_n \ell} + 1 \right)}. \end{equation} $$

where $n=1$ corresponds to $\texttt{AT}_1$ ($c_n = 2/3$) and $n=2$ to $\texttt{AT}_2$ ($c_n = 1/2$).

plt.subplots(figsize=(12, 4))
plt.subplot(1, 2, 1)
fluid_volume = []
surface_energy = []
# Open the file for reading
with (out_dir / "log.txt").open() as fd:
    # Iterate over the lines
    for _i, line in enumerate(fd):
        match_surface_energy = re.search(
            r"""Surface energy: (\d+\.\d*) Pressure work: (\d+\.\d*)  at time: (\d+\.\d*)""",
            line,
        )
        if match_surface_energy:
            surface_energy.append(float(match_surface_energy.group(1)))
            fluid_volume.append(float(match_surface_energy.group(3)))

plt.grid(linestyle="dashed")
plt.xlabel("Volume")
plt.ylabel("Crack length")
plt.plot(fluidVolume_analytical, length_analytical, "black", label="Closed form")
plt.plot(
    fluid_volume,
    np.array(surface_energy[:]) / Gc_ref / 2,
    "bo",
    fillstyle="none",
    label="Phase-field",
)
legend = plt.legend(loc="lower right")

plt.subplot(1, 2, 2)
fluid_volume = []
pressure = []
# Open the file for reading
with (out_dir / "log.txt").open() as fd:
    # Iterate over the lines
    for _i, line in enumerate(fd):
        match_pressure = re.search(
            r"""Pressure: (\d+\.\d*) at time: (\d+\.\d*)""", line
        )
        if match_pressure:
            fluid_volume.append(float(match_pressure.group(2)))
            pressure.append(float(match_pressure.group(1)))


plt.xlabel("Volume")
plt.ylabel("$p_f/p_c$")
plt.plot(fluidVolume_analytical, pressure_analytical, "black", label="Closed form")
plt.plot(
    np.array(fluid_volume[:]),
    np.array(pressure[:]) / P_c,
    "g<",
    fillstyle="none",
    label="Phase-field",
)
plt.grid(linestyle="dashed")
legend = plt.legend(loc="upper right")
plt.show()

png 

plt.subplots(figsize=(12, 4))
plt.subplot(1, 2, 1)
plt.grid(linestyle="dashed")
plt.plot(
    fluidVolume_analytical[1:],
    (
        abs(length_analytical[1:] - np.array(surface_energy[:]) / (2 * Gc_ref))
        / (np.array(surface_energy[:]) / (2 * Gc_ref))
    )
    * 100,
    "-.ob",
    fillstyle="none",
    label="Closed form",
)
plt.ylim([0.0, 10])
plt.xlabel("Volume")
plt.ylabel(
    r"$\frac{|a_\mathrm{num}-{a}_\mathrm{ana}|}{{a}_\mathrm{num}}\times 100\%$",
    fontsize=14,
)

plt.subplot(1, 2, 2)
plt.grid(linestyle="dashed")
plt.plot(
    fluidVolume_analytical[1:],
    (abs(pressure_analytical[1:] - np.array(pressure[:]) / P_c) / pressure[:]) * 100,
    "-.<g",
    fillstyle="none",
    label="Closed form",
)
plt.ylim([0.0, 10])
plt.xlabel("Volume")
plt.ylabel(
    r"$\frac{|p_\mathrm{num}-{p}_\mathrm{ana}|}{{p}_\mathrm{num}}\times 100\%$",
    fontsize=14,
)
plt.show()

png

In order to reduce computation time, we perform the simulation with a coarse mesh; the results for the $\texttt{AT}_1$ Model with a mesh size of $h=0.001$ are provided below.

$\texttt{AT}_1$ Model:

Phase field versus analytical solution for fracture length and pressure evolution
Phase field versus analytical solution for fracture length and pressure evolution, $\texttt{AT}_1$.

Error between the Phase field and analytical solution for fracture length and pressure evolution.
Error between the Phase field and analytical solution for fracture length and pressure evolution, $\texttt{AT}_1$.

Hydraulic Fracturing Animation (Using Phase Field Approach)

import pyvista as pv

pv.set_plot_theme("document")
pv.set_jupyter_backend("static")
filename = f"results_h_{h:0.4f}_{phasefield_model}"
reader = pv.get_reader(f"{out_dir}/" + filename + ".pvd")

plotter = pv.Plotter(shape=(1, 2), border=False)
plotter.open_gif(f"{out_dir}/Kregime_Propagating.gif")
for time_value in reader.time_values:
    reader.set_active_time_value(time_value)
    mesh = reader.read()[0]
    sargs = {
        "title": "Phase field",
        "title_font_size": 16,
        "label_font_size": 12,
        "n_labels": 5,
        "position_x": 0.25,
        "position_y": 0.15,
        "fmt": "%.1f",
        "width": 0.5,
    }
    p = pv.Plotter(shape=(1, 2), border=False)
    clim = [0, 1.0]
    points = mesh.point_data["phasefield"].shape[0]
    xs = mesh.points[:, 0]
    ys = mesh.points[:, 1]
    pf = mesh.point_data["phasefield"]
    plotter.clear()
    plotter.add_mesh(
        mesh,
        scalars=pf,
        show_scalar_bar=True,
        colormap="coolwarm",
        clim=clim,
        scalar_bar_args=sargs,
        lighting=False,
    )
    plotter.add_text(f"Time: {time_value:0.02f}", color="black")

    plotter.view_xy()
    plotter.write_frame()

plotter.close()
DRI3 not available
failed to load driver: zink

Phase Field Profile at Last Time Step

mesh = reader.read()[0]

points = mesh.point_data["phasefield"].shape[0]
xs = mesh.points[:, 0]
ys = mesh.points[:, 1]
pf = mesh.point_data["phasefield"]

clim = [0, 1.0]
sargs = {
    "title": "Phase field",
    "title_font_size": 16,
    "label_font_size": 12,
    "n_labels": 5,
    "position_x": 0.25,
    "position_y": 0.0,
    "fmt": "%.1f",
    "width": 0.5,
}
plotter = pv.Plotter(shape=(1, 2), border=False)
plotter.add_mesh(
    mesh,
    scalars=pf,
    show_edges=False,
    show_scalar_bar=True,
    colormap="coolwarm",
    clim=clim,
    scalar_bar_args=sargs,
    lighting=False,
)

plotter.view_xy()
plotter.camera.zoom(1.5)
plotter.window_size = [1000, 500]
plotter.show()
DRI3 not available
failed to load driver: zink

png

References

[1] Detournay, Emmanuel. Mechanics of hydraulic fractures. Annual review of fluid mechanics 48 (2016): 311-339.

[2] Bourdin, Blaise, Chukwudi Chukwudozie, and Keita Yoshioka. A variational approach to the numerical simulation of hydraulic fracturing. In SPE annual technical conference and exhibition. OnePetro, 2012.

[3] Sneddon, Ian Naismith, and Morton Lowengrub. Crack problems in the classical theory of elasticity. 1969, 221 P (1969).

[4] Griffith, Alan Arnold. VI. The phenomena of rupture and flow in solids. Philosophical transactions of the royal society of london. Series A, containing papers of a mathematical or physical character 221, no. 582-593 (1921): 163-198.

[5] Yoshioka, Keita, Francesco Parisio, Dmitri Naumov, Renchao Lu, Olaf Kolditz, and Thomas Nagel. Comparative verification of discrete and smeared numerical approaches for the simulation of hydraulic fracturing. GEM-International Journal on Geomathematics 10, no. 1 (2019): 1-35.

Next
Pre-notched shear test

This article was written by Mostafa Mollaali, Keita Yoshioka. If you are missing something or you find an error please let us know.
Generated with Hugo 0.122.0 in CI job 430699 | Last revision: March 3, 2023