An example of the coupled thermal hydraulic processes in the FEBEX type repository

• Parabolic/HT/StaggeredCoupling/ADecovalexTHMCBasedHTExample/th_decovalex.prj

Problem description

This example is based on the The TASK D_THM1 of the DECOVALEX-THMC project. The TASK D_THM1 of the DECOVALEX-THMC project studies the coupled thermal hydraulic and mechanical (THM) processes in the FEBEX type nuclear waster repository. In the FEBEX type repository, nuclear waster canisters are stored in the drifts excavated in the deep rock mass of granite, which is fully water saturated, and they are sealed with bentonite. Initially, the bentonite, the sealing material, is partially saturated. TASK D_THM1 defines a 2D model about the FEBEX type repository \cite BirEtAl:2008. In this example, TASK D_THM1 is simplified in order to test the staggered scheme for TH process in OGS. The simplifications are

1. resizing the domain to an area that can represent the near field of an installed nuclear water canister,
2. assuming the bentonite is fully saturated from the beginning,
3. ignoring the mechanical process.

With such simplifications, the geometry of the present example is illustrated in the following figure:

In the above figure, the domain in the annulus sector represents the sealing material, bentonite. A heat power, which is generated by the nuclear waste with one million year variation, is applied onto the inner arc of the annulus sector. On the top boundary, the boundary conditions are $p=4.3 ⋅ 10^6\ \mathrm{Pa}, T=294\ \mathrm{K}$. While on the bottom boundary, the boundary conditions are set as $p=4.7 ⋅ 10^6\ \mathrm{Pa}, T=319\ \mathrm{K}$. The initial conditions are given as $p=4.7 ⋅ 10^6\ \mathrm{Pa}, T=298\ \mathrm{K}$.

The material properties are shown in the following table:

Material properties

Property	Value	Unit
Bentonite
Density	kg/m3	1600
Porosity	-	0.01
Thermal conductivity	W/(mK)	3
Specific heat capacity	J/(kgK)	3
Saturated permeability	m2	2.0 ⋅ 10−21
Granite
Density	kg/m3	2700
Porosity	-	0.41
Thermal conductivity	W/(mK)	3
Specific heat capacity	J/(kgK)	900
Saturated permeability	m2	10−17

Solution

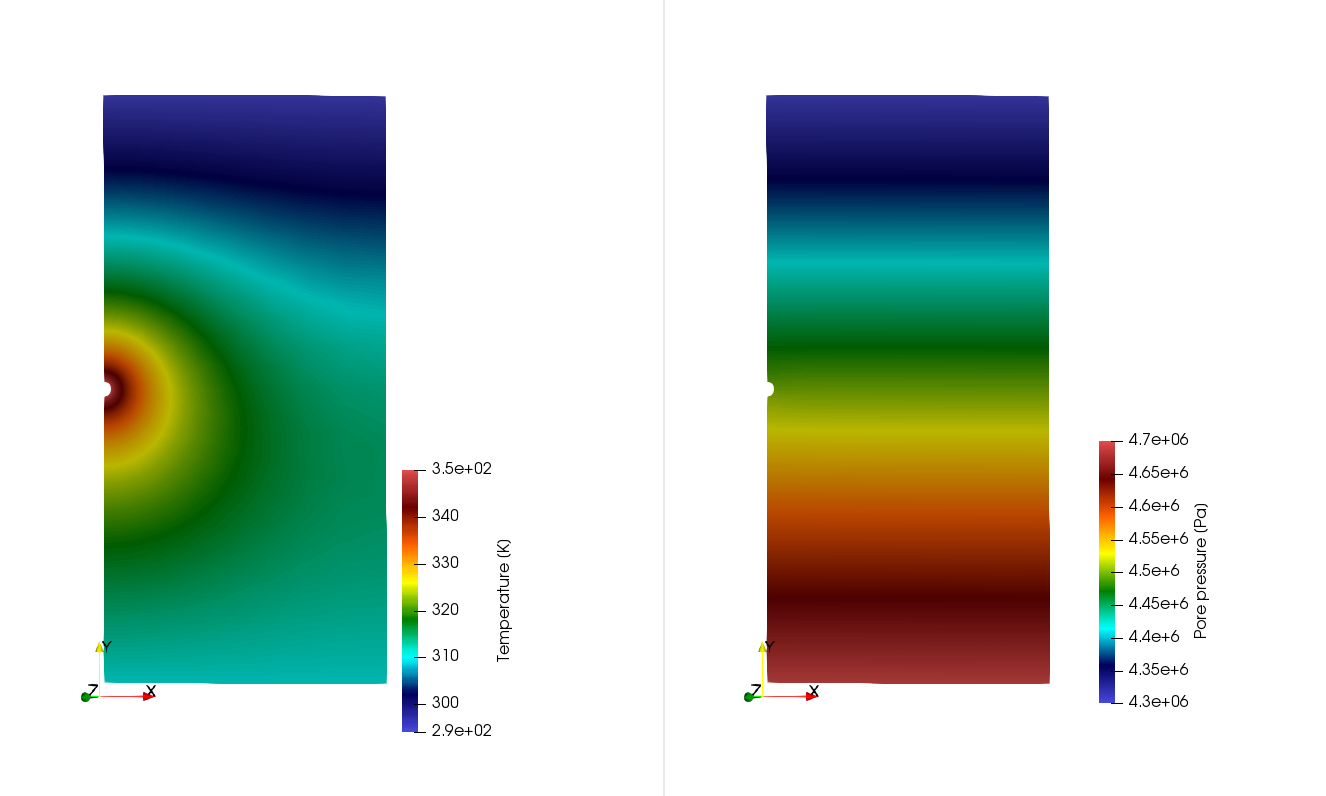
As the reference results, the temperature and pressure distributions in the domain at the time of 18 years are shown in the following figure, in which the thermal convection effective can be seen clearly.

Reference

Birkholzer, J. and Rutqvist, J. and Sonnenthal, E. and Barr, D. (2008): {DECOVALEX-THMC} {P}roject, {T}ask {D}: {L}ong-term permeability/porosity changes in the {EDZ} and near field due to {THM} and {THC} processes in volcanic and crystalline-bentonite systems.