Classical transport example: using the full upwind stabilization

• Parabolic/HT/ClassicalTransportExample/classical_transport_example_full_upwind.prj

Purpose

This example tests the full upwind stabilization scheme, the type name of which is FullUpwind.

Theory

For the full upwind scheme, we consider the general advection term of the advection diffusion transport equation:

$$ \nabla \cdot ( u \mathbf{v}), $$

where $u$ can be temperature $ T$ or mass component concentration $C$, and $\mathbf{v}$ is the fluid velocity. This means $\nabla \cdot \mathbf{v}$ may not be zero, or physically the fluid flow may be compressible.

The discretized weak form of that advection term takes the form

$$ \int_{\Omega_e} \nabla \cdot ( u \mathbf{v}) \phi_i \mathrm{d} \Omega = \int_{\Omega_e} \nabla \cdot ( u \mathbf{v} \phi_i) \mathrm{d} \Omega - \int_{\Omega_e} \nabla \phi_i \cdot ( u \mathbf{v} ) \mathrm{d} \Omega $$

with $\phi_i$ the test function. The first term on the right hand side can be converted to boundary integration according to the Green’s theorem as

$$ \int_{\Omega_e} \nabla \cdot ( u \mathbf{v} \phi_i) \mathrm{d} \Omega = \int_{\partial\Omega_e} ( u \mathbf{v} \phi_i) \cdot \mathbf{n} \mathrm{d} \Gamma $$

with $\mathbf{n}$ the normal to the boundary surface. That boundary integration is a part of Neumann boundary condition. Therefore what left for the element integration is

$$ -\int_{\Omega_e} \nabla \phi_i \cdot ( u \mathbf{v} ) \mathrm{d} \Omega, $$

which is denoted as $R_i$ hereafter.

Based on the scheme introduced by Dalen [1], the full upwind scheme evaluates the following flux related quantity for each node

$$ q_i = -\int_{\Omega_e} \nabla \phi_i \cdot \mathbf{v} \mathrm{d} \Omega $$

to determine whether it is an upwind node. If $q_i>0$, node $i$ is at upwind position.

Let

$$ q_{up} = \sum_{q_i >= 0} q_i u_i $$

be the total flux at the upwind nodes, and

$$ q_{down} = \sum_{q_i < 0} q_i $$

be the total flux related quantity at the down nodes, we can approximate the discretized weak form of the advection term as:

$$ \begin{eqnarray} R_i \approx \begin{cases} q_i\,u_i,\forall q_i >= 0, \newline q_i \frac{q_{up}}{q_{down}},\forall q_i < 0 \end{cases} = \begin{cases} q_i\,u_i,\forall q_i \>= 0\newline \frac{1}{q_{down}} q_i {\sum_{q_j >= 0} (q_j u_j)},\forall q_i < 0 \end{cases}=\tilde R_i. \end{eqnarray} $$

The above approximation defines the full upwind scheme of the advection term of the advection diffusion transport equation for the FEM analysis. Obviously, we see that

$$ \begin{eqnarray} \sum_i \tilde R_i &=& \sum_{q_i >= 0} q_i u_i + \sum_{q_i < 0} \frac{1}{q_{down}} q_i {\sum_{q_j >= 0} (q_j u_j)}\newline &=& \sum_{q_i >= 0} q_i u_i + \frac{\sum_{q_i < 0} q_i}{q_{down}} {\sum_{q_j >= 0} (q_j u_j)} = q_{up}-q_{up} = 0, \end{eqnarray} $$

which means that the nodal mass balance of element is guaranteed.

Example and its results

The example is described in Classical transport example: using the isotropic diffusion stabilization.

The following two figures compare the example results with the analytical solution and that are obtained by using the isotropic diffusion stabilization.

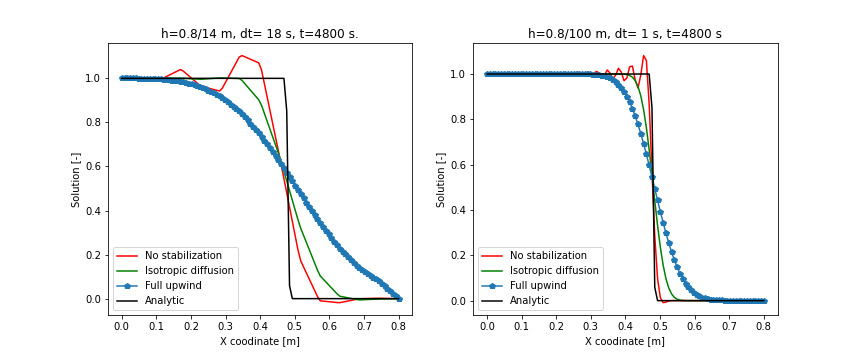
From the figures we can see that the full upwind scheme adds more diffusion than the isotropic diffusion scheme does.

Reference

[1] Dalen, V., 1979. Simplified finite-element models for reservoir flow problems. Society of Petroleum Engineers Journal, 19(05), pp.333-343.