One dimensional heat transport in stationary flow
Problem description
We consider one dimensional heat transport in stationary flow in a porous medium. This benchmark was first introduced as an exercise of Geoenergy Modeling I – Geothermal Processes in Fractured Porous Media for OGS 5.
Numerical setting
The size of the domain is 1 m in the horizontal direction. The material properties of fluid are:
| Property | Value | Unit |
|---|---|---|
| Density | 1000 | kg/m^3 |
| Viscosity | 1.e-3 | Pa⋅s |
| Specific heat capacity | 4182 | J/K/kg |
| Thermal conductivity | 0.6 | W/(m⋅K) |
The material properties of porous medium are:
| Property | Value | Unit |
|---|---|---|
| Density | 2850 | kg/m^3 |
| Specific heat capacity | 0 | J/K/kg |
| Thermal conductivity | 0 | W/(m⋅K) |
The intrinsic permeability is 1.e-11 m^2. Since the flow equation is steady state, the porosity $n$ is not applied in that equation. We set $n=1$ in order to use the specific heat capacity and the thermal conductivity of fluid as the effective ones.
The initial boundary conditions are T(0)=0 °C and p(0)=1.e+5 Pa.
At the left boundary, a constant temperature of T=1 °C and a constant pressure of p=1.01e+5 Pa are prescribed. At the right boundary condition, there is no heat flux and the pressure is set as the initial one. The pressure boundary conditions lead to a stationary flow with a velocity of 1.e-5 m/s.
The time duration is 5.e+4 s. A fixed time step size of 250 s is used for the temporal discretization.
This example is also set as one of the benchmarks of ThermoHydroMechanics (THM) and ThermoRichardsMechanics (TRM), respectively. In order to provide a reference result for the same benchmark of THM and TRM, a 2D domain of 1 m $\times$ 0.1 m is used, which is discretised into 3$\times$39 quadrilateral elements.
Result
The temperature distribution at t= 5.e+4 s together with the mesh is
illustrated in the following figure:
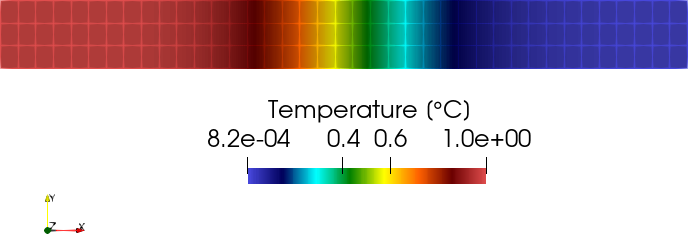
The temperature profile at t= 5.e+4 s along a horizontal line in the
2D domain is given in the following figure:
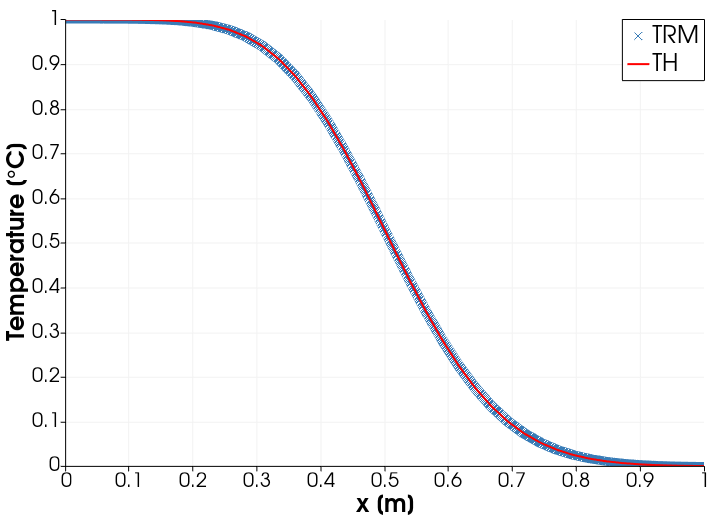
This article was written by Wenqing Wang. If you are missing something or you find an error please let us know.
Generated with Hugo 0.122.0
in CI job 570044
|
Last revision: April 17, 2025
Commit: Rewrite using ranges 1ed34f4
| Edit this page on