Classical transport example: using the isotropic diffusion stabilization

• Parabolic/HT/ClassicalTransportExample/classical_transport_example.prj

Purpose

This example tests the simplest stabilization scheme, i.e. that with the isotropic diffusion balance approach. In OGS, the type name of that stabilization scheme is IsotropicDiffusion.

Theory

Stabilization is the numerical approach to eliminate the spatial oscillations produced by the Galerkin finite element method for the advection diffusion transport equation.

The advection diffusion transport equation takes the form

$$ \frac{\partial u}{\partial t} - \nabla(\mathbf{K}\nabla u) + {\mathbf v}\cdot \nabla u = Q $$

with $u$ the primary variable, $\mathbf v$ the fluid velocity, $\mathbf{K}$ the diffusion coefficient.

The stabilization scheme adds an artificial isotropic balancing dissipation to the diffusion coefficient to force the Péclet number to be smaller than 1. The isotropic balancing dissipation is defined as

$$ \mathbf{K}_{\delta} = \frac{1}{2}\alpha ||\mathbf v||h \mathbf I $$

with $\alpha \in [0,1]$ the tuning parameter, $h$ the element size (e.g. the maximum edge length of element), and $\mathbf I$ the identity matrix.

Example description

The example defines the mass transport in liquid flow with a constant liquid velocity in 1D domain.

The domain size is 0.8 m. The initial value of the primary variable is 0. The Dirichlet boundary conditions are applied on the left and right boundaries with respective values 1.0 and 0.0. The constant velocity is 1.e-4 m/s. The diffusion coefficient is $10^{-9}$ m/s. The analysis duration is 7200 s.

Derived by Ogata, A. and Banks [1], the analytical solution of the example is

$$ c(x, t)=\frac{1}{2}\left(\mathrm{erfc}\left(\frac{x-v t}{2\sqrt{K t}}\right) +\mathrm{exp}(vx/K) \mathrm{erfc}\left(\frac{x+v t}{2\sqrt{K t}}\right) \right) $$

where $v$ and $K$ are the scalar values of $\mathbf v$ and $\mathbf K$, respectively. Since the given diffusion coefficient is too small, the term with $\mathrm {exp}$ function is dropped due to overflow. This leads to

$$ c(x, t) \approx \frac{1}{2} \mathrm{erfc}\left(\frac{x-v t}{2\sqrt{K t}}\right) $$

The example is for mass transport process. To tailor it for running with HT process in OGS, the input material data are defined such as

• for liquid phase, the density, the viscosity and the specific heat capacity are set to 1 and the thermal conductivity is $10^{-9}$.
• for solid phase all input data are zero,
• The porosity is set to 1.

The tuning parameter for IsotropicDiffusion takes small value 0.15, while the cutoff velocity is 0.

Note: With the same material data, the example is also tested with ThermoHydroMechanics process by fixing displacement to zero at all mesh nodes.

Result

With the Galerkin finite element method, fine spatial and temporal discretizations give more accurate results, however, it can lead to spatial oscillation when Péclet number is large.

To investigate such phenomenon, different spatial and temporal discretizations are considered for the example.

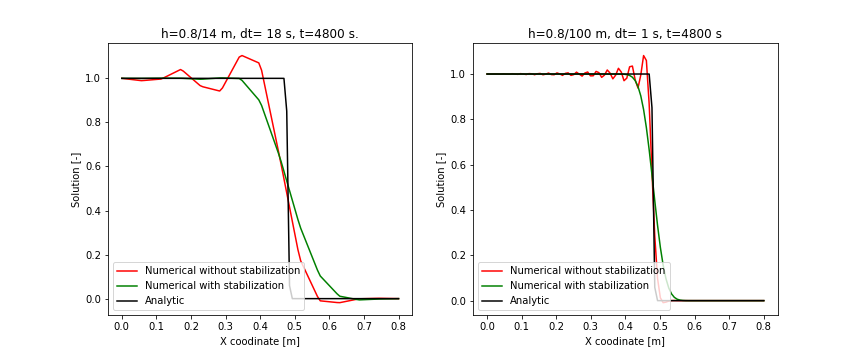
The following figures show the benchmark results with two different spatial and temporal discretization sets. Both results show that the stabilization of IsotropicDiffusion eliminates the spatial oscillation.

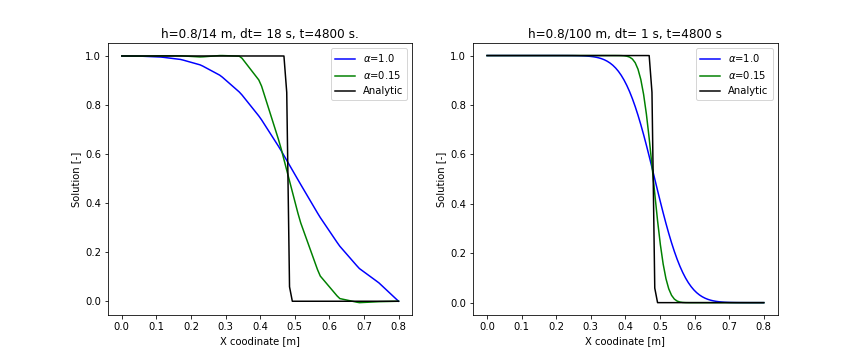
The following figure compares the simulation results obtained with $\alpha=0.15$ and its maximum value 1, respectively:

Reference

[1] Ogata, A. and Banks, R.B., 1961. A solution of the differential equation of longitudinal dispersion in porous media: fluid movement in earth materials. US Government Printing Office.