Two-layer diffusion problem
1. Two-layer diffusion problem
1.1 Problem description
In waste repositories, radionuclide release can be expected after rupture of waste canisters to occur in the engineered barrier system, which contains multiple layers of materials and host rocks. In this benchamrk, a tracer (HTO) diffusion process through a two-layer barrier is simulated. The barrier is comprised of a bentonite buffer layer and an opalinus clay (OPA) layer.
Over the one-dimensional model domain, the diffusion process of HTO can be described with the following governing equation:
$$ \frac{\partial \left( \phi c\right)}{\partial t} = \frac{\partial}{\partial x} \left( \phi \mathrm{D_p} \frac{\partial c}{\partial x} \right), $$where $c$ [mol/m$^3$] represents the HTO concentration. $\mathrm{D_p}$ [m$^2$/s] is the pore diffusion coefficient for HTO, and $\phi$ [-] is the porosity of the media.
1.2 Model setups
The computational domain is assumed to be 20 meters long. It consists of a 0.625 meter thick layer of bentonite buffer, and the rest is filled with OPA. The simulation time is one million years. Initially, the entire domain is assumed to be solute free, i.e. $c_{\mathrm{ini}}(x, 0) = 0$. The inlet concentration is held at 1 mol/L throughout the simulation, i.e. $c(0, t) = 1$ mol/L. In the numerical model, the spatial domain is discretized by linear line elements with a length of 0.005 meter each. The time step size of 1000 years is used in the simulation. The discretized governing equation is iteratively solved using the Newton-Raphson method.
The table below summarizes the parameters used in the simulation.
| Parameter | Value | Unit |
|---|---|---|
| Porosity of bentonite $\phi_{\mathrm{b}}$ | 0.36 | - |
| Porosity of OPA $\phi_{\mathrm{OPA}}$ | 0.12 | - |
| Pore diffusion coefficient in bentonite $\mathrm{D_{p,b}}$ | 5.55e-10 | m$^2$/s |
| Pore diffusion coefficient in OPA $\mathrm{D_{p,OPA}}$ | 8.33e-11 | m$^2$/s |
| Time step size $\Delta t$ | 1e3 | year |
| Grid size $\Delta x$ | 0.01 | m |
Notes: The parameter values are sourced from Nagra (2002).
1.3 Results
Analytical solution
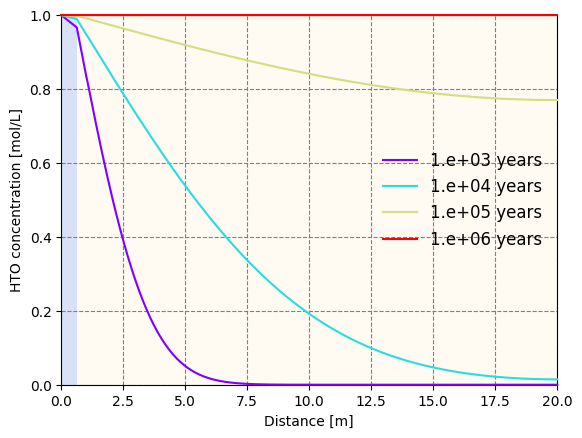
For a two-layer diffusion problem, it is difficult to obtain the exact analytical solution. Instead, Carr and Turner (2016) presented a semi-analytical solution for this type of problem and released the corresponding MATLAB script for public usage.
Here we provide a MATLAB script through which we can compute the concentration profiles along the two-layer domain. The following figure illustrates the concentration profiles at $t$ = 10$^3$, 10$^4$, 10$^5$, and 10$^6$ years (see calculated values in SemiAnalyticalSolutionResults.csv).
import os
import matplotlib.pyplot as plt
import numpy as np
import pandas as pd
import vtuIO
from IPython.display import Image
from matplotlib.pyplot import cm# plot semi-analytical solution
# Time [year]
time = np.array([1e3, 1e4, 1e5, 1e6])
result_file = "./SemiAnalyticalSolutionResults.csv"
soln = pd.read_csv(
result_file,
sep=",",
header=None,
skiprows=0,
names=["x", "1e3", "1e4", "1e5", "1e6"],
index_col=False,
)
def plot_analytical_solutions():
fig, ax = plt.subplots()
ax.set_xlim((0, 20))
ax.set_ylim((0, 1))
plt.xlabel("Distance [m]")
plt.ylabel("HTO concentration [mol/L]")
color_map = iter(cm.rainbow(np.linspace(0, 1, len(time))))
# represent the bentonite layer
plt.axvspan(0, 0.625, facecolor="royalblue", alpha=0.2)
# represent the OPA host rock
plt.axvspan(0.625, 20, facecolor="orange", alpha=0.05)
for col_name, t, color in zip(soln[["1e3", "1e4", "1e5", "1e6"]], time, color_map):
ax.plot(
soln["x"],
soln[col_name],
linestyle="-",
lw=1.5,
label=str(np.format_float_scientific(t)) + " years",
c=color,
zorder=10,
clip_on=False,
)
ax.legend(frameon=False, loc="center right", numpoints=1, fontsize=12, ncol=1)
ax.xaxis.grid(color="gray", linestyle="dashed")
ax.yaxis.grid(color="gray", linestyle="dashed")
plot_analytical_solutions()
Numerical solution
Correspondingly, the OGS input files of this 1D mass transport benchmark can be found here.
Then, the numerical solution by OpenGeoSys is plotted against the semi-analytical solution for comparison.
# Run OGS simulation
prj_name = "1D_MultiLayerDiffusion"
prj_file = f"{prj_name}.prj"
from pathlib import Path
out_dir = Path(os.environ.get("OGS_TESTRUNNER_OUT_DIR", "_out"))
if not out_dir.exists():
out_dir.mkdir(parents=True)
print(f"ogs {prj_file} > out.txt")
! ogs {prj_file} -o {out_dir} > {out_dir}/out.txt
# Read simulation results
pvdfile = vtuIO.PVDIO(f"{out_dir}/{prj_name}.pvd", dim=1)
def plot_simulation_results():
fig, ax = plt.subplots()
ax.set_xlim((0, 20))
ax.set_ylim((0, 1))
plt.xlabel("Distance [m]")
plt.ylabel("HTO concentration [mol/L]")
# represent the bentonite layer
plt.axvspan(0, 0.625, facecolor="royalblue", alpha=0.2)
# represent the OPA host rock
plt.axvspan(0.625, 20, facecolor="orange", alpha=0.05)
color_map = iter(cm.rainbow(np.linspace(0, 1, len(time))))
# Plot semi-analytical solutions
for col_name, _t, color in zip(soln[["1e3", "1e4", "1e5", "1e6"]], time, color_map):
ax.plot(
soln["x"],
soln[col_name],
linestyle="-",
lw=1.5,
c=color,
zorder=10,
clip_on=False,
)
# Add simulation results
x = np.linspace(0, 20, num=201)
color_map = iter(cm.rainbow(np.linspace(0, 1, len(time))))
for t, color in zip(time, color_map):
c_t = pvdfile.read_set_data(
t * 3.1536e7, "HTO", data_type="point", pointsetarray=[(i, 0, 0) for i in x]
)
plt.plot(
x,
c_t,
label="Sim. " + str(np.format_float_scientific(t)) + " years",
color=color,
marker="o",
markevery=5,
linestyle="",
zorder=10,
clip_on=False,
)
ax.legend(frameon=False, loc="center right", numpoints=1, fontsize=12, ncol=1)
ax.xaxis.grid(color="gray", linestyle="dashed")
ax.yaxis.grid(color="gray", linestyle="dashed")
plot_simulation_results()ogs 1D_MultiLayerDiffusion.prj > out.txt
WARNING: Default interpolation backend changed to VTK. This might result in
slight changes of interpolated values if defaults are/were used.
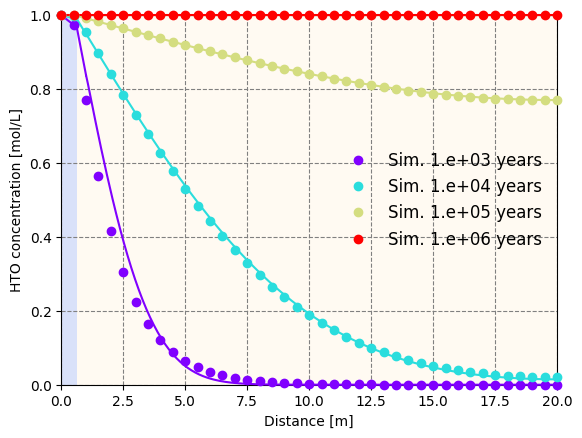
In the first time step, the semi-analytical and numerical solutions do not agree so well. As the time step progresses, they begin to agree more closely.
Mass flux calculation
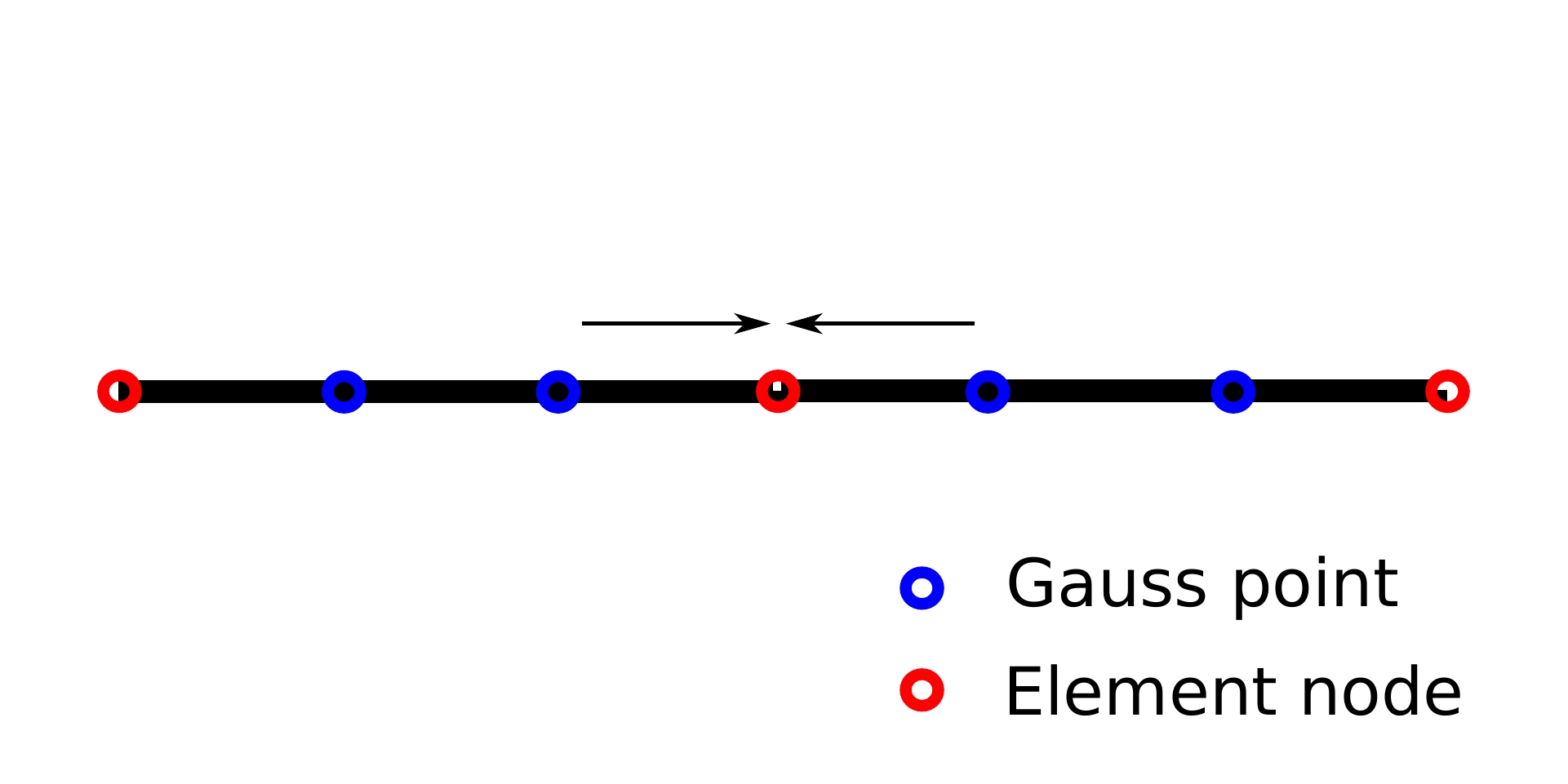
Here is a sketch that shows how we calculate the molar flux at the node.
from IPython.display import display
display(Image(filename="./sketch_molar_flux_calculation.jpg", width=400))
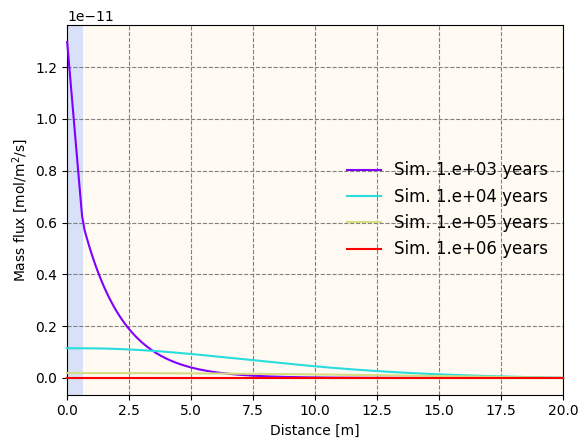
Additionally, we compute the molar flux profiles at $t$ = 10$^3$, 10$^4$, 10$^5$, and 10$^6$ years. The implementation of molar flux output can be viewed at this link.
def plot_molar_flux():
fig, ax = plt.subplots()
ax.set_xlim((0, 20))
plt.xlabel("Distance [m]")
plt.ylabel("Mass flux [mol/m$^2$/s]")
# represent the bentonite layer
plt.axvspan(0, 0.625, facecolor="royalblue", alpha=0.2)
# represent the OPA host rock
plt.axvspan(0.625, 20, facecolor="orange", alpha=0.05)
# plot total mass flux
x = np.linspace(0, 20, num=201)
color_map = iter(cm.rainbow(np.linspace(0, 1, len(time))))
for t, color in zip(time, color_map):
c_t = pvdfile.read_set_data(
t * 3.1536e7,
"HTOFlux",
data_type="point",
pointsetarray=[(i, 0, 0) for i in x],
)
plt.plot(
x,
c_t,
label="Sim. " + str(np.format_float_scientific(t)) + " years",
color=color,
linestyle="-",
lw=1.5,
zorder=10,
clip_on=False,
)
ax.legend(frameon=False, loc="center right", numpoints=1, fontsize=12, ncol=1)
ax.xaxis.grid(color="gray", linestyle="dashed")
ax.yaxis.grid(color="gray", linestyle="dashed")
plot_molar_flux()
References
Nagra, 2002. Project Opalinus Clay: Models, Codes and Data for Safety Assessment. Technical Report NTB 02–06. Nagra, Switzerland.
E. J. Carr and I. W. Turner (2016), A semi-analytical solution for multilayer diffusion in a composite medium consisting of a large number of layers, Applied Mathematical Modelling, 40: pp. 7034–7050. http://dx.doi.org/10.1016/j.apm.2016.02.041
Credits:
Renchao Lu, Dmitri Naumov, Lars Bilke, Christoph Lehmann, Haibing Shao
This article was written by Renchao Lu, Dmitri Naumov, Lars Bilke, Christoph Lehmann, Haibing Shao. If you are missing something or you find an error please let us know.
Generated with Hugo 0.122.0
in CI job 449919
|
Last revision: March 9, 2022

