Gas Diffusion
 |
 |
 |
|---|
1D Linear Diffusion
Analytical Solution
The solution of the diffusion equation for a point x in time t reads:
$ c(x,t) = \left(c_0-c_i\right)\operatorname{erfc}\left(\frac{x}{\sqrt{4Dt}}\right)+c_i$
where $c$ is the concentration of a solute in mol$\cdot$m$^{-3}$, $c_i$ and $c_b$ are initial and boundary concentrations; $D$ is the diffusion coefficient of the solute in water, x and t are location and time of solution.
import numpy as np
from scipy.special import erfc
# Analytical solution of the diffusion equation
def Diffusion(x, t):
if (
not isinstance(t, int)
and not isinstance(t, np.float64)
and not isinstance(t, float)
):
# In order to avoid a division by zero, the time field is increased
# by a small time unit at the start time (t=0). This should have no
# effect on the result.
tiny = np.finfo(np.float64).tiny
t[t < tiny] = tiny
d = np.sqrt(4 * D * t)
return (c_b - c_i) * erfc(x / d) + c_i
# Utility-function transforming mass fraction into conctration
def concentration(xm_WL):
xm_CL = 1.0 - xm_WL
return xm_CL / beta_cMaterial properties and problem specification
# Henry-coefficient and compressibility of solution
H = 7.65e-6
beta_c = 2.0e-6
# Diffusion coefficient
D = 1.0e-9
# Boundary and initial gas pressures
pGR_b = 9e5
pGR_i = 1e5
# Boundary and initial concentration
c_b = concentration(1.0 - (beta_c * H * pGR_b))
c_i = concentration(1.0 - (beta_c * H * pGR_i))Numerical Solution
import os
from pathlib import Path
out_dir = Path(os.environ.get("OGS_TESTRUNNER_OUT_DIR", "_out"))
if not out_dir.exists():
out_dir.mkdir(parents=True)from ogs6py.ogs import OGS
model = OGS(INPUT_FILE="diffusion.prj", PROJECT_FILE=f"{out_dir}/modified.prj")
model.replace_text(1e7, xpath="./time_loop/processes/process/time_stepping/t_end")
model.replace_text(
5e4, xpath="./time_loop/processes/process/time_stepping/timesteps/pair/delta_t"
)
# Write every timestep
model.replace_text(1, xpath="./time_loop/output/timesteps/pair/each_steps")
model.write_input()
# Run OGS
model.run_model(logfile=f"{out_dir}/out.txt", args=f"-o {out_dir} -m .")OGS finished with project file /var/lib/gitlab-runner/builds/F1XUyv4cx/0/ogs/build/release-all/Tests/Data/TH2M/H/diffusion/diffusion/modified.prj.
Execution took 25.842841625213623 s
Project file written to output.
# Colors
cls1 = ["#4a001e", "#731331", "#9f2945", "#cc415a", "#e06e85", "#ed9ab0"]
cls2 = ["#0b194c", "#163670", "#265191", "#2f74b3", "#5d94cb", "#92b2de"]import vtuIO
pvdfile = vtuIO.PVDIO(f"{out_dir}/result_diffusion.pvd", dim=2)
# Get all written timesteps
time = pvdfile.timesteps
# Select individual timesteps for c vs. x plots for plotting
time_steps = [1e6, 2e6, 4e6, 6e6, 8e6, 1e7]
# 'Continuous' space axis for c vs. x plots for plotting
length = np.linspace(0, 1.0, 101)
# Draws a line through the domain for sampling results
x_axis = [(i, 0, 0) for i in length]
# Discrete locations for c vs. t plots
location = [0.01, 0.05, 0.1, 0.2, 0.5, 1.0]WARNING: Default interpolation backend changed to VTK. This might result in
slight changes of interpolated values if defaults are/were used.
# The sample locations have to be converted into a 'dict' for vtuIO
observation_points = {"x=" + str(x): (x, 0.0, 0.0) for x in location}
# Samples concentration field at the observation points for all timesteps
c_over_t_at_x = pvdfile.read_time_series("xmWL", observation_points)
for key in c_over_t_at_x:
x = c_over_t_at_x[key]
c_over_t_at_x[key] = concentration(x)
# Samples concentration field along the domain at certain timesteps
c_over_x_at_t = []
for t in range(len(time_steps)):
c_over_x_at_t.append(
concentration(
pvdfile.read_set_data(time_steps[t], "xmWL", pointsetarray=x_axis)
)
)import matplotlib.pyplot as plt
plt.rcParams["figure.figsize"] = (14, 4)
# Plot of concentration vs. time at different locations
fig1, (ax1, ax2) = plt.subplots(1, 2)
ax1.set_xlabel("$t$ / s", fontsize=12)
ax1.set_ylabel("$c$ / mol m$^{-3}$", fontsize=12)
ax2.set_xlabel("$t$ / s", fontsize=12)
ax2.set_ylabel(r"$\epsilon_\mathrm{abs}$ / mol m$^{-3}$", fontsize=12)
label_x = []
for key, _c in c_over_t_at_x.items():
x = observation_points[key][0]
label_x.append(key + r" m")
# numerical solution
ax1.plot(
time,
c_over_t_at_x[key],
color=cls1[location.index(x)],
linewidth=3,
linestyle="--",
)
# analytical solution
ax1.plot(
time,
Diffusion(x, time),
color=cls1[location.index(x)],
linewidth=2,
linestyle="-",
)
# absolute error
err_abs = Diffusion(x, time) - c_over_t_at_x[key]
ax2.plot(
time,
err_abs,
color=cls1[location.index(x)],
linewidth=1,
linestyle="-",
label=key + r" m",
)
# Hack to force a custom legend:
from matplotlib.lines import Line2D
custom_lines = []
for i in range(6):
custom_lines.append(Line2D([0], [0], color=cls1[i], lw=4))
custom_lines.append(Line2D([0], [0], color="black", lw=3, linestyle="--"))
custom_lines.append(Line2D([0], [0], color="black", lw=2, linestyle="-"))
label_x.append("OGS-TH2M")
label_x.append("analytical")
ax1.legend(custom_lines, label_x, loc="right")
ax2.legend()
fig1.savefig(f"{out_dir}/diffusion_c_vs_t.pdf")
# Plot of concentration vs. location at different times
fig1, (ax1, ax2) = plt.subplots(1, 2)
ax1.set_xlabel("$x$ / m", fontsize=12)
ax1.set_ylabel("$c$ / mol m$^{-3}$", fontsize=12)
ax1.set_xlim(0, 0.4)
ax2.set_xlabel("$x$ / m", fontsize=12)
ax2.set_ylabel(r"$\epsilon$ / mol $m^{-3}$", fontsize=12)
ax2.set_xlim(0, 0.4)
# Plot concentration over domain at five moments
label_t = []
for t in range(len(time_steps)):
s = r"$t=$" + str(time_steps[t] / 1e6) + r"$\,$Ms"
label_t.append(s)
# numerical solution
ax1.plot(length, c_over_x_at_t[t], color=cls2[t], linewidth=3, linestyle="--")
# analytical solution
ax1.plot(
length,
Diffusion(length, time_steps[t]),
color=cls2[t],
linewidth=2,
linestyle="-",
)
# absolute error
err_abs = Diffusion(length, time_steps[t]) - c_over_x_at_t[t]
ax2.plot(length, err_abs, color=cls2[t], linewidth=1, linestyle="-", label=s)
custom_lines = []
for i in range(6):
custom_lines.append(Line2D([0], [0], color=cls2[i], lw=4))
custom_lines.append(Line2D([0], [0], color="black", lw=3, linestyle="--"))
custom_lines.append(Line2D([0], [0], color="black", lw=2, linestyle="-"))
label_t.append("OGS-TH2M")
label_t.append("analytical")
ax1.legend(custom_lines, label_t, loc="right")
ax2.legend()
fig1.savefig(f"{out_dir}/diffusion_c_vs_x.pdf")
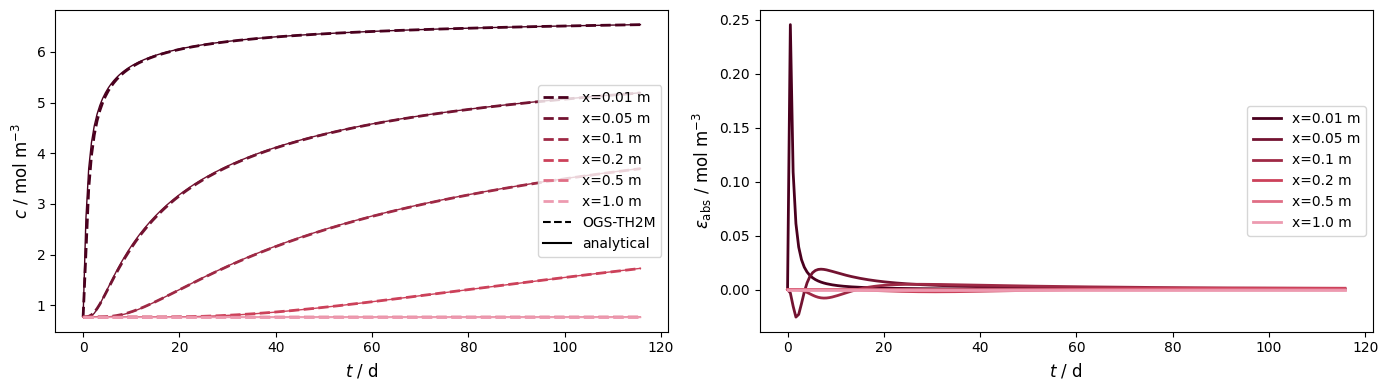
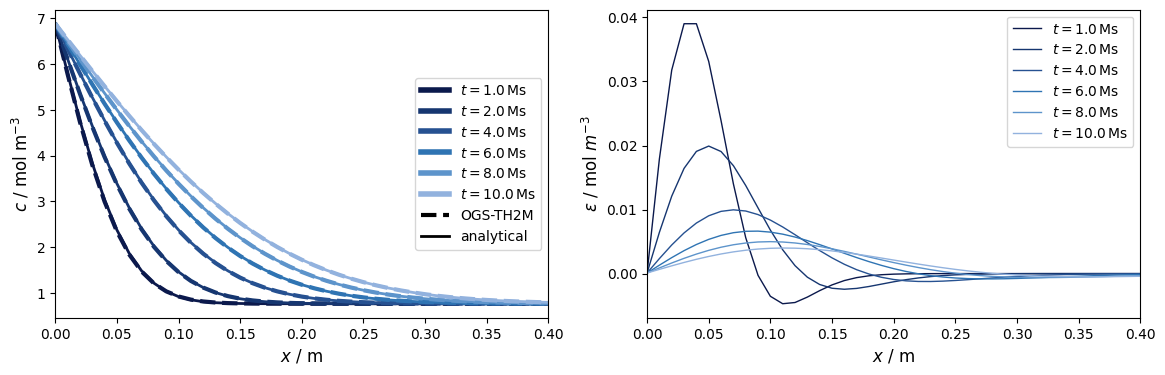
The numerical approximation approaches the exact solution quite well. Deviations can be reduced if the resolution of the temporal discretisation is increased.
This article was written by Norbert Grunwald. If you are missing something or you find an error please let us know.
Generated with Hugo 0.122.0
in CI job 449919
|
Last revision: October 19, 2022

