Precipitation/dissolution equilibrium reactions in a saturated column
Overview
This benchmark was firstly described in Kolditz et al. (2012) as a reactive transport benchmark including precipitation and dissolution reactions along a saturated column of calcite which is fluxed with a diluted solution of MgCl$_2$. Three different codes (OGS-5#ChemApp, OGS-5#IPhreeqc and OGS-5#GEMS) were used in that exercise.
Kolditz et al. (2012) considered that all reactions occurred at thermodynamic equilibrium. Later on, in He et al. (2015) and Jang et al. (2018), the incorporation of kinetic rates for reaction precipitations in OGS-5#IPhreeqc was investigated and compared with the modelling results obtained with OGS-5#ChemApp and PHREEQC.
Very briefly, the studied system consists on a column of 0.5 m, initially containing crushed calcite (CaCO$_3$(s)), which is continuously fluxed with a 1 millimolar (mmol/L) magnesium chloride (MgCl$_2$) solution at pH = 7 and 25°C during 350 min (~ 5.8h) at a constant flow rate of 0.18 L (or a Darcy velocity (q) of $3\times10^{-6}$ m/s, considering a cross-sectional area of 1 m$^2$).
Previously, the column had been packed giving a mean bulk density and porosity of 1.80 kg/L and 0.32, respectively. Additionally, the column was saturated and equilibrated by injecting pure water giving a saturated solution with respect calcite and pH = 9.9.
Numerical approach
Reactive component$^{(*)}$ transport processes in saturated porous media illustrated in this benchmark have been possible by integrating IPhreeqc v.3.5.0 module (Parkhurst et al. 2013) in OGS-6. The operator-splitting (OS) model formulation (Strang et al. 1968) with a sequential non-iterative approach (SNIA) has been used for the implementation.
In a first step, the mass balance equation describing the component transport within the fluid is solved by a parabolic operator (see HC-Process.pdf). Then, in a second step, the nonlinear algebraic equations describing the equilibrium chemical reactions between the aqueous components and the solid (i.e. mass action law) are solved with a modified Newton-Raphson method implemented in IPhreeqc.
($^*$Note: component denotes a chemical species that belongs to the minimum number of independent chemical species necessary to completely describe their mass).
In this way, a conservative mass transport equation for component $i$ is solved
$$ \begin{equation} \frac{\partial C_i}{\partial t} = - \nabla\left(v C_i\right) + \nabla\left(D_i \nabla C_i \right) + Q_i, \end{equation} $$$$ \begin{equation} \frac{\partial S C_i}{\partial t} = \Gamma_i \left(C_i ... C_m\right), \end{equation} $$
with $C_i$ (mol m$^{-3}$) standing for the molar concentration of component $i$, $v$ (m s$^{-1}$) for the pore velocity in the fluid phase, $D_h$ (m$^2$ s$^{-1}$) for the dispersion tensor of component $i$, $Q_i$ (mol m$^{-3}$ s$^{-1}$) for a source/sink term, and $\Gamma_i$ (C$_1$ …C$_m$) (mol m$^{-3}$ s$^{-1}$) being a source/sink term for component $i$ due to chemical reactions with $m$ other components. The Scheidegger dispersion tensor is implemented in two dimensions as
$$ \begin{equation} D_{kl} = \alpha_T |v| \delta_{kl} + \left( \alpha_L - \alpha_T \right) \frac{v_k v_l}{|v|} + D_e, \end{equation} $$where $\alpha_L$ (m) and $\alpha_T$ (m) are the longitudinal and transversal dispersion length, respectively. $\delta_{kl}$ (–) is the Kronecker symbol, $v_{k,l}$ (m s$^{-1}$) is the fluid pore velocity in direction $k$,$l$, and $D_e$ (m$^2$ s$^{-1}$) is the molecular diffusion coefficient.
Model setup
A one-dimensional (1D) model domain of 0.5 m discretised into 100 uniform elements has been selected for the spatial discretization of the system. Dirichlet (constant concentration) and Neumannn (no flux) boundary condition are defined for the upstream inflow and the downstream, respectively. A longitudinal dispersivity of 0.0067 m and a time step size of 100 s have been taken into account in the simulation. See Figure below:

Schematic representation of the model setup and parameters.
Thermodynamic data for hydrolysis, aqueous speciation, and dissolution/precipitation reactions between Mg, Ca, Cl, and carbonate were selected from version 12/07 of the PSI/NAGRA chemical thermodynamic database (Thoenen et al. 2014). Although several other minerals containing Mg and Ca were available in the PSI/NAGRA database (i.e. magnesite), only two solids were allowed to precipitate or dissolve in the studied system (calcite and dolomite (CaMg(CO$_3$)$_2$)).
Model results
A comparison of the results obtained with OGS-6#IPhreeqc and OGS-5#IPhreeqc at the end of the simulation is shown in the Figures below.
At the simulated time, it can be clearly seen that the MgCl$_2$ solution front has penetrated ~0.3m of the column resulting in the dissolution of calcite and dolomite precipitation. Total aqueous concentration and solid profiles obtained of OGS-6 are in good agreement with those of OGS-5. The absolute error in terms of component concentrations is $2.15\times10^{-5}$ (Cl), $1.13\times10^{-5}$ (Mg), and $4.57\times10^{-6}$ (Ca). Additionally, pH profiles calculated with both codes are in good agreement.
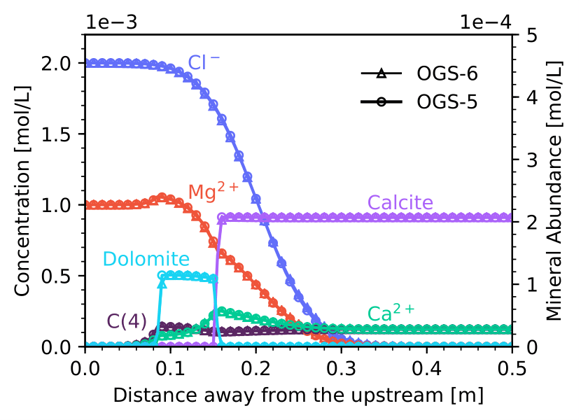
Total aqueous concentration and solid profiles obtained with OGS-6#IPhreeqc (empty triangle symbol) and OGS-5#IPhreeqc (empty circle symbol) at 350 min. (C(4) = total carbonate)
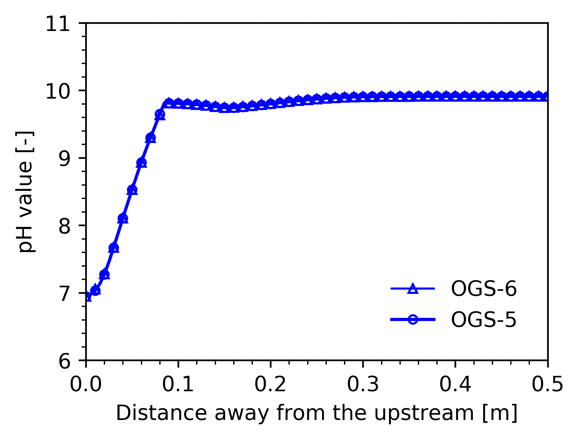
pH value profiles obtained with OGS-6#IPhreeqc (empty triangle symbol) and OGS-5#IPhreeqc (empty circle symbol) at 350 min.
Literature
He, W., Beyer, C., Fleckenstein, J.H., Jang, E., Kolditz, O., Naumov, D., Kalbacher, T., 2015. A parallelization scheme to simulate reactive transport in the subsurface environment with OGS#IPhreeqc 5.5.7-3.1.2. Geosci. Model Dev. 8 (10), 3333 - 3348
Jang, E., Boog, J., He, W., Kalbacher, T., 2018. OpenGeoSys Tutorial. Computational hydrology III: OGS#IPhreeqc coupled reactive transport modeling SpringerBriefs in Earth System Sciences. Springer International Publishing, Cham, 103 pp.
Kolditz, O., Görke, U.-J., Shao, H., Wang, W., 2012. Thermo-Hydro-Mechanical-Chemical Processes in Porous Media: Benchmarks and Examples, Lecture notes in computational science and engineering. Springer. ISBN: 3642271766.
Parkhurst, D.L., Appelo, C.A.J., 2013. Description of Input and Examples for PHREEQC Version 3 - a Computer Program for Speciation, Batch-reaction, One-dimensional Transport, and Inverse Geochemical Calculations.
Thoenen, T., Hummel,W., Berner, U., Curti, E., 2014. The PSI/Nagra Chemical Thermodynamic Data Base 12/07. PSI Report 14-04, Villigen, Switzerland.
This article was written by Vanessa Montoya, Renchao Lu. If you are missing something or you find an error please let us know.
Generated with Hugo 0.147.9
in CI job 577984
|
Last revision: May 22, 2025
Commit: Remove deprecated TES process 6477209a
| Edit this page on