LargeDeformations: Torsion of a hyperelastic bar
 |
 |
|---|
Convergence under large deformations (preliminary)
In this benchmark we impose large tensile and torsional deformations on a hyperelastic prismatic bar. The material model is a Saint-Venant-Kirchhoff material law for initial testing.
# HIDDEN…
(click to toggle)
# HIDDEN
import numpy as np
import matplotlib.pyplot as plt
from matplotlib import cm
from ogs6py import ogs
import os
import pyvista as pv
pv.set_plot_theme("document")
pv.set_jupyter_backend("static")
# Some plot settings
plt.rcParams["lines.linewidth"] = 2.0
plt.rcParams["lines.color"] = "black"
plt.rcParams["legend.frameon"] = True
plt.rcParams["font.family"] = "serif"
plt.rcParams["legend.fontsize"] = 14
plt.rcParams["font.size"] = 14
plt.rcParams["axes.spines.right"] = False
plt.rcParams["axes.spines.top"] = False
plt.rcParams["axes.spines.left"] = True
plt.rcParams["axes.spines.bottom"] = True
plt.rcParams["axes.axisbelow"] = True
plt.rcParams["figure.figsize"] = (8, 6)Boundary conditions
The bar of dimensions $1 \times 1 \times 6$ m³ is stretched by $\lambda = 1.5$ in the axial direction and twisted by 180°. The following graph illustrates the torsion bc.
R = lambda x, y: np.sqrt(x**2 + y**2)…
(click to toggle)
R = lambda x, y: np.sqrt(x**2 + y**2)
def phi(x, y):
theta = np.arctan2(y, x)
return np.where(theta < 0, theta + 2 * np.pi, theta)
def u(x, y):
ux = R(x, y) * np.cos(phi(x, y) + np.pi / 20) - x
uy = R(x, y) * np.sin(phi(x, y) + np.pi / 20) - y
return [ux, uy]
x = np.linspace(-0.5, 0.5, 10)…
(click to toggle)
x = np.linspace(-0.5, 0.5, 10)
y = x.copy()
X, Y = np.meshgrid(x, y)
fig, ax = plt.subplots()
ax.plot(X, Y, marker="s", color="red", ls="", alpha=0.5)
ax.quiver(X, Y, u(X, Y)[0], u(X, Y)[1], pivot="mid")
ax.set_aspect("equal")
ax.set_xlabel("$x$ / m")
ax.set_ylabel("$y$ / m")
ax.set_title("Displacement-controlled torsion on face of prismatic bar")
fig.tight_layout();
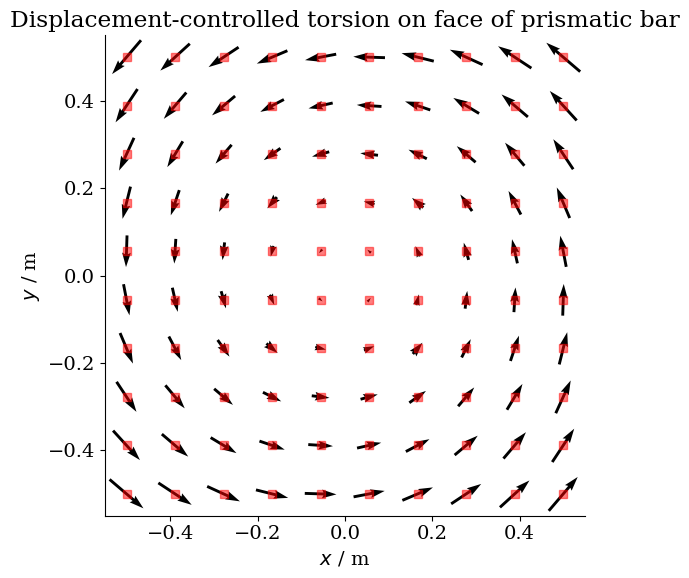
import os…
(click to toggle)
import os
from pathlib import Path
out_dir = Path(os.environ.get("OGS_TESTRUNNER_OUT_DIR", "_out"))
if not out_dir.exists():
out_dir.mkdir(parents=True)
model = ogs.OGS(PROJECT_FILE="bar1to6_torsion.prj")…
(click to toggle)
model = ogs.OGS(PROJECT_FILE="bar1to6_torsion.prj")
model.run_model(logfile=f"{out_dir}/out.txt", args=f"-o {out_dir}")…
(click to toggle)
model.run_model(logfile=f"{out_dir}/out.txt", args=f"-o {out_dir}")OGS finished with project file bar1to6_torsion.prj.
Execution took 3.239091634750366 s
Project file written to output.
Let’s plot the result.
reader = pv.get_reader(f"{out_dir}/bar1to6_torsion.pvd")…
(click to toggle)
reader = pv.get_reader(f"{out_dir}/bar1to6_torsion.pvd")
print(reader.time_values)
reader.set_active_time_value(0.05)
mesh = reader.read()[0][0.0, 0.01, 0.02, 0.03, 0.04, 0.05]
plotter = pv.Plotter(shape=(1, 2), window_size=[1000, 500])…
(click to toggle)
plotter = pv.Plotter(shape=(1, 2), window_size=[1000, 500])
warped = mesh.warp_by_vector("displacement")
plotter.subplot(0, 0)
plotter.add_mesh(mesh, show_edges=True, show_scalar_bar=False, color=None, scalars=None)
plotter.show_bounds(
ticks="outside", xtitle="x / m", ytitle="y / m", ztitle="z / m", font_size=10
)
plotter.add_axes()
plotter.view_isometric()
plotter.add_text("undeformed", font_size=10)
plotter.subplot(0, 1)
plotter.add_mesh(
warped, show_edges=True, show_scalar_bar=None, color=None, scalars="displacement"
)
plotter.view_isometric()
plotter.add_text("deformed", font_size=10)
plotter.show()
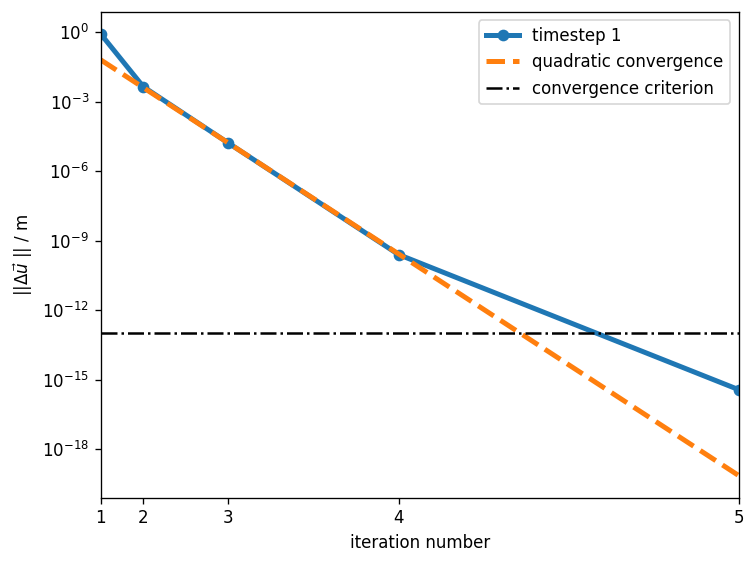
Convergence
What we’re more interested in, is the convergence behaviour over time. The large deformations were applied in only 5 load steps to challenge the algorithm.
df = model.parse_out(f"{out_dir}/out.txt", filter="convergence_newton_iteration")…
(click to toggle)
df = model.parse_out(f"{out_dir}/out.txt", filter="convergence_newton_iteration")
last_ts = df["time_step"].values[-1]…
(click to toggle)
last_ts = df["time_step"].values[-1]
fig, ax = plt.subplots()
for i in range(1, last_ts + 1):
timestep = df[df["time_step"] == i]
ax.plot(
timestep["iteration_number"],
timestep["dx"],
label="timestep %i" % i,
color="darkblue",
alpha=i / (last_ts + 1),
)
ax.axhline(1e-13, ls="--", label="convergence criterion")
ax.plot([7, 8, 7, 7], [1e-6, 1e-12, 1e-12, 1e-6], color="black")
ax.text(7.3, 2e-12, "1")
ax.text(6.7, 1e-9, "2")
ax.set_yscale("log")
ax.set_xlabel("iteration number")
ax.set_ylabel("$|| \Delta \\vec{u}$ || / m")
ax.legend()
fig.tight_layout();
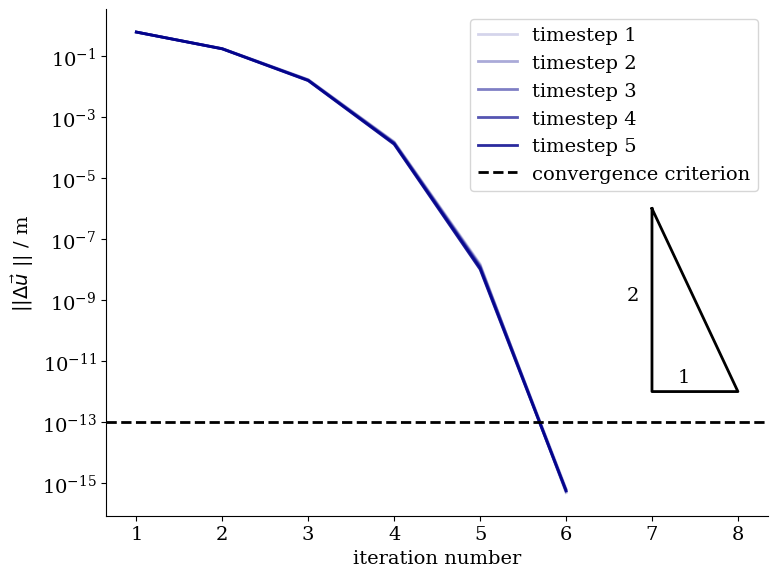
We observe quadratic convergence in the proximity of the solution supporting the implementation of the geometric stiffness matrix.
This article was written by Thomas Nagel. If you are missing something or you find an error please let us know.
Generated with Hugo 0.122.0
in CI job 487174
|
Last revision: March 2, 2023


