Mandel-Cryer Effect
Mandel-Cryer Effect
This is a classical example to demonstrate the effect of hydromechanical coupling in a poroelastic medium. For more details we refer to a textbook (Verruijt, 2009), in which also the analytical solution is derived. As domain we consider a sphere, by symmetry we need to simulate only an octant.
The boundary conditions of hydraulics are atmospheric pressure on the sphere surface and impermeable elsewhere. The boundary conditions of mechanics are an overburden (Neumann) applied as step load on the sphere surface at initial time $t=0$. The remaining sides are fixed in normal direction (Dirichlet).
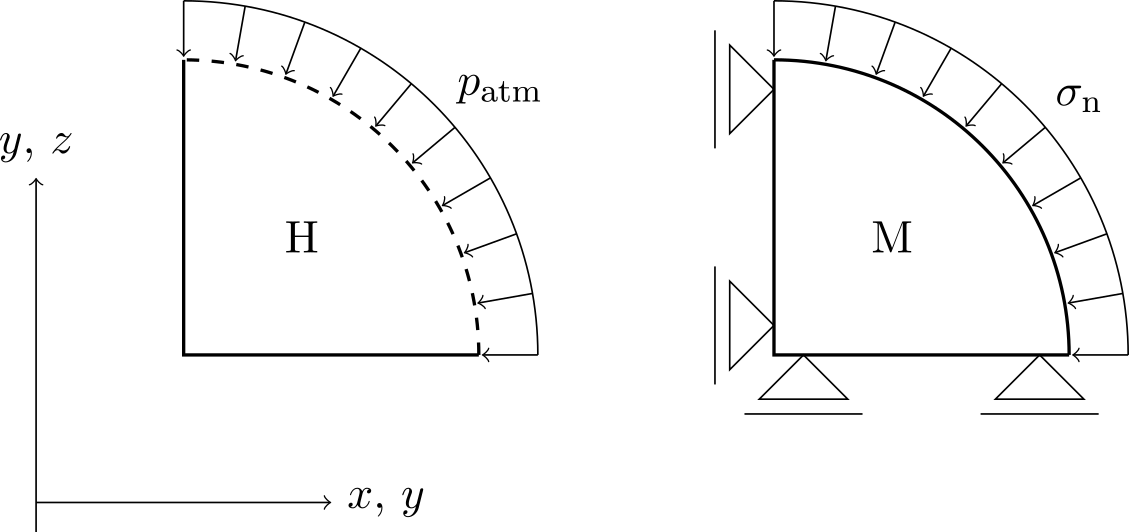
The material is isotropic, linear elastic. Solid and fluid are assumed to be incompressible. In its initial state the sphere is not deformed and there is ambient pressure everywhere. A sudden load increase on the surface is instantly transferred on the pore pressure, whereas the solid needs time to deform, until it carries the load. Since the pore fluid is squeezed out of the outer layers first, they act like a tightening belt and consequently the pressure in the center rises, it may even exceed the value of the applied load. Finally the pore pressure approaches to ambient pressure.
All parameters are concluded in the following tables.
Material Properties
| Property | Value | Unit |
|---|---|---|
| Fluid density | $10^3$ | kg/m$^3$ |
| Viscosity | $10^{-3}$ | Pa$\cdot$s |
| Porosity | $0.2$ | - |
| Permeability | $10\cdot 10^{-12}$ | m$^2$ |
| Young’s modulus (bulk) | $10\cdot 10^6$ | Pa |
| Poisson ratio (bulk) | $0.1$ | - |
| Biot coefficient | $1.0$ | - |
| Solid density | $2.5\cdot 10^3$ | kg/m$^3$ |
| Overburden | $1000$ | Pa |
| Atmospheric pressure | $0$ | Pa |
Dimensions and Discretization
| Property | Value | Unit |
|---|---|---|
| Radius | $0.4$ | m |
| Finite Elements | $8741$ | Taylor-Hood tetrahedra |
| Time step | $10^{-2}$ | s |
| Coupling scheme parameter | $0.7774$ | - |
Numerical Simulation
# Create output path if it doesn't exist yet…
(click to toggle)
# Create output path if it doesn't exist yet
import os
from pathlib import Path
out_dir = Path(os.environ.get("OGS_TESTRUNNER_OUT_DIR", "_out"))
if not out_dir.exists():
out_dir.mkdir(parents=True)
# Import OGS class…
(click to toggle)
# Import OGS class
from ogs6py.ogs import OGS
# Initiate an OGS-object
# Pass it the project file and set an output file
model = OGS(INPUT_FILE="MandelCryerStaggered.prj", PROJECT_FILE=f"{out_dir}/MandelCryerStaggered_modified.prj")
# Increase end time
t_end = 1.5
model.replace_text(t_end, xpath="./time_loop/processes/process/time_stepping/t_end")
model.write_input()
# Run OGS
model.run_model(logfile=f"{out_dir}/out.txt", args=f"-o {out_dir} -m .")OGS finished with project file /var/lib/gitlab-runner/builds/F1XUyv4cx/1/ogs/build/release-all/Tests/Data/HydroMechanics/StaggeredScheme/MandelCryer/mandelcryer/MandelCryerStaggered_modified.prj.
Execution took 766.2360136508942 s
Project file written to output.
Results
import vtuIO…
(click to toggle)
import vtuIO
import numpy as np
# Load the result
pvdfile = vtuIO.PVDIO(f"{out_dir}/results_MandelCryerStaggered.pvd", dim=3)
# Get point field names
fields = pvdfile.get_point_field_names()
print(fields)
# Get all written timesteps
time = pvdfile.timesteps['displacement', 'epsilon', 'pressure', 'sigma', 'velocity']
import matplotlib.pyplot as plt…
(click to toggle)
import matplotlib.pyplot as plt
# Define observation points
observation_points = {'center':(0, 0, 0)}
pressure = pvdfile.read_time_series('pressure', observation_points)
# Plot soil temperature
fig, ax1 = plt.subplots(figsize=(10, 8))
ax1.plot(time, pressure['center'], color="tab:orange")
ax1.set_ylabel('Pressure (Pa)', fontsize=20)
ax1.set_xlabel('Time (s)', fontsize=20)
ax1.set_xlim(0, t_end)
ax1.set_ylim(0, 1500)
ax1.grid()
fig.supxlabel('Pressure at center of sphere')
plt.show()
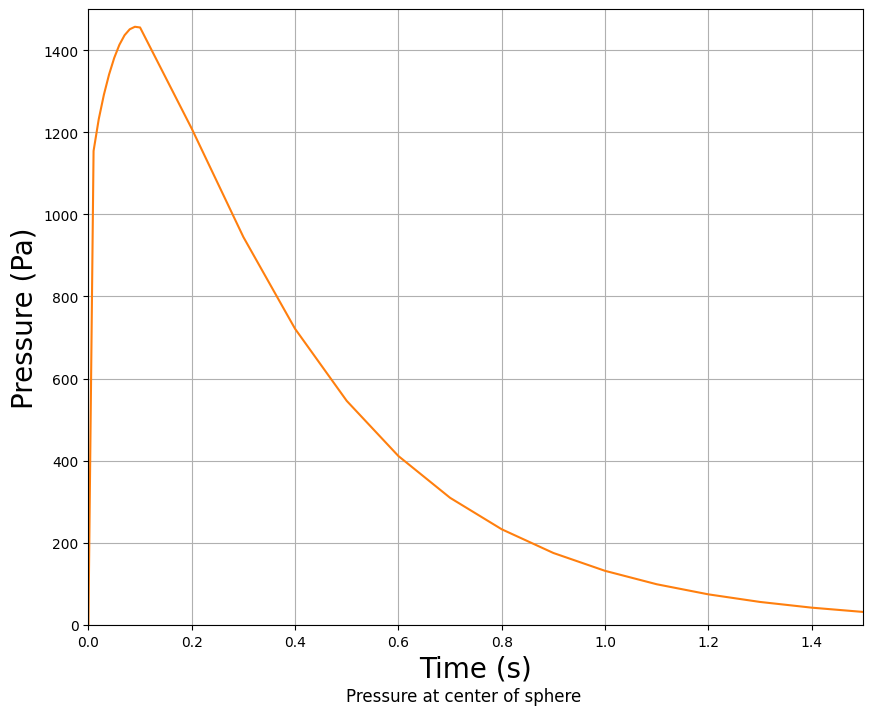
As predicted, the pressure in the center exceeds the applied load and then levels out.
For more details about the staggered scheme we refer to the user guide - conventions.
References
[1] Verruijt, A. (2009): An introduction to soil dynamics. Springer Science and Business Media, DOI: https://doi.org/10.1007/978-90-481-3441-0, https://link.springer.com/book/10.1007/978-90-481-3441-0
This article was written by Dominik Kern, Frieder Loer. If you are missing something or you find an error please let us know.
Generated with Hugo 0.122.0
in CI job 487174
|
Last revision: January 25, 2022


