Consolidation benchmark with the staggered scheme

• HydroMechanics/StaggeredScheme/ConsolidationBenchmark/consolidation_benchmark.prj

---

This is an example to test the fixed stress splitting with the approach of fixed stress rate over time step (see the algorithms in Injection and Production in 1D Linear Poroelastic Medium with the Staggered Scheme).

We consider a porous column bounded by rigid and impermeable walls, except on its top where a mechanical pressure load $\sigma_0$ is prescribed and which is free to drain. Suppose that the length of the column is H. The boundary and initial conditions for the problem are

$$ \eqalign{ &\sigma =\sigma_0, p = 0\, \text{on}\, x=0,\cr &u=0, \dfrac{\partial p}{\partial x}=0\, \text{on}\, x=H,\cr &\sigma = p = 0\, \text{at}\, t=0. } $$

By omitting the body force, assuming zero liquid storage and homogeneous material, the analytical solution for this problem can be found in [1,2] as

$$ \eqalign{ &\sigma_D=-1+\sum_{n=0}^{\infty} \dfrac{2}{M}\sin(Mx_D)\exp^{-M^2t_D}, \cr &u_D=1-x_D-\sum_{n=0}^{\infty} \dfrac{2}{M}\cos(Mx_D)\exp^{-M^2t_D}, \cr &p_D =\sigma_D+1, } $$

where the $x_D = x/H$, $t_D = (\lambda + 2\mu)kt/\eta H^2$, and $M = 1/2\pi(2n + 1)$ are the non-dimensional quantities, and $\sigma_D = \sigma/p_0$, $u_D = u(\lambda + 2 G)/p_0 H$, and $p_D = p/p_0$ are the dimensionless effective stress, the displacement, and the pore pressure, respectively. $\lambda$ is the Lame constant, and $G$ is the shear modulus.

Since the storage is zero, the pressure change in this example is purely driven by the strain change.

In this example, we see that the densities can be arbitrary non-zero values. The values of the required material parameters are given in the following table:

Parameter	Value	Unit
Young’s modulus	$3\cdot 10^4$	Pa
Poisson’s ratio	$0.2$	-
Permeability	$10^{-10}$	$\text{m}^2$
Viscosity	$10^{-3}$	Pa s

The mechanical load on the top boundary is 1000 Pa, i.e. $\sigma_0 = -1000$ Pa.

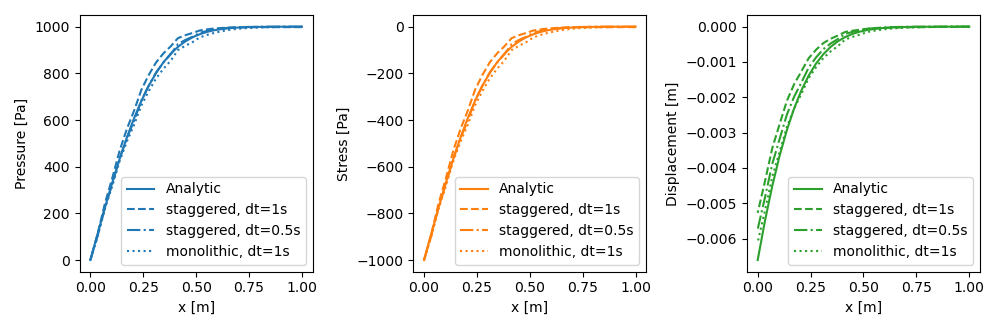
In the following figures, the solutions at $t=10$ s obtained by using the staggered scheme with fixed stress rate over time step, the monolithic scheme, and analytic approach are compared.

The figures show that for the staggered scheme with fixed stress rate over time step, the solutions with $dt=0.5$ s are quite close to the analytical ones.

References

[1] Murad, Márcio A and Loula, Abimael FD (1992): Improved accuracy in finite element analysis of Biot's consolidation problem. Computer Methods in Applied Mechanics and Engineering, vol. 95, p. 359--382, Elsevier, DOI:10.1016/0045-7825(92)90193-N

[2] Korsawe, Johannes and Gerhard, Starke and Wang, Wenqing and Kolditz, Olaf (2006): Finite element analysis of poro-elastic consolidation in porous media: Standard and mixed approaches. Computer Methods in Applied Mechanics and Engineering, vol. 195, p. 1096–-1115, Elsevier, DOI:10.1016/j.cma.2005.04.011