Non-isothermal test
Problem description
We solve a homogeneous damage under non-isothermal conditions. The size of the cubic model is 1$\times$1$\times1$ mm. Detailed model description can refer the latest published benchmark book “Thermo-Hydro-Mechanical-Chemical Processes in Fractured Porous Media: Modelling and Benchmarking” (Chapter 9.7 – A Phase-Field Model for Brittle Fracturing of Thermo-Elastic Solids).
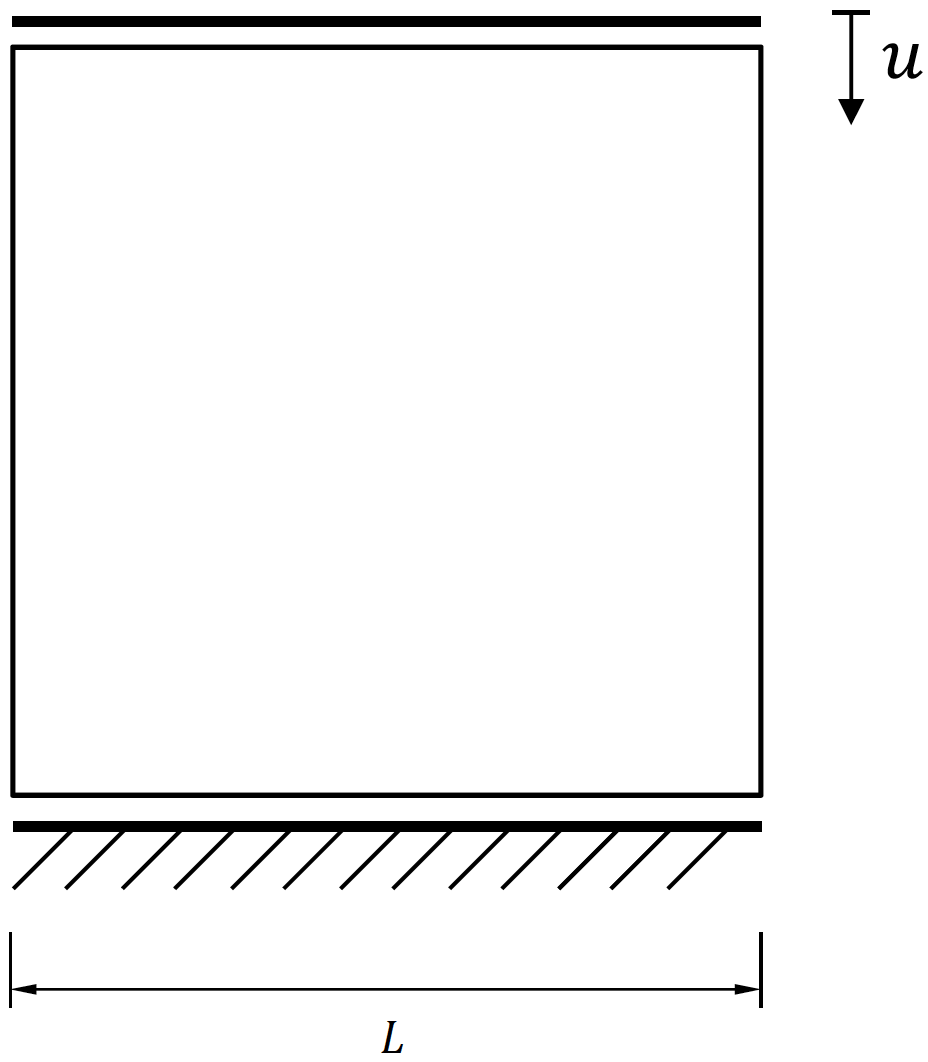
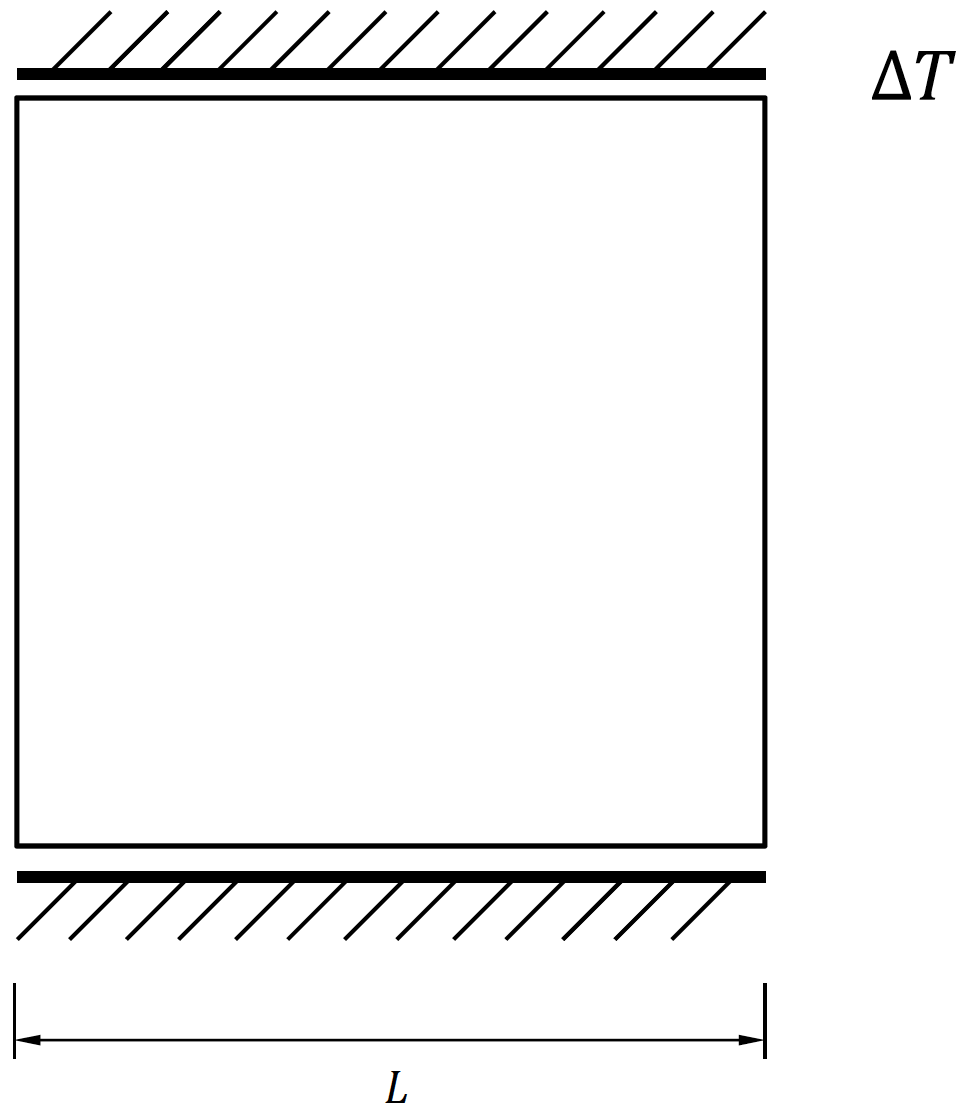
A unconfined compression test was applied as a comparison. The thermal expansion test was implemented by imposing a temperature increase to the domain while the top surface of the model was held in place. The temperature loading was chosen to achieve the same compressive load as that imposed in the unconfined compression test.
Models, results, and evaluation
Results show Phase-Field evolution in the thermo-mechanical case can follow the mechanical case, and both solutions correspond to the analytical solution:
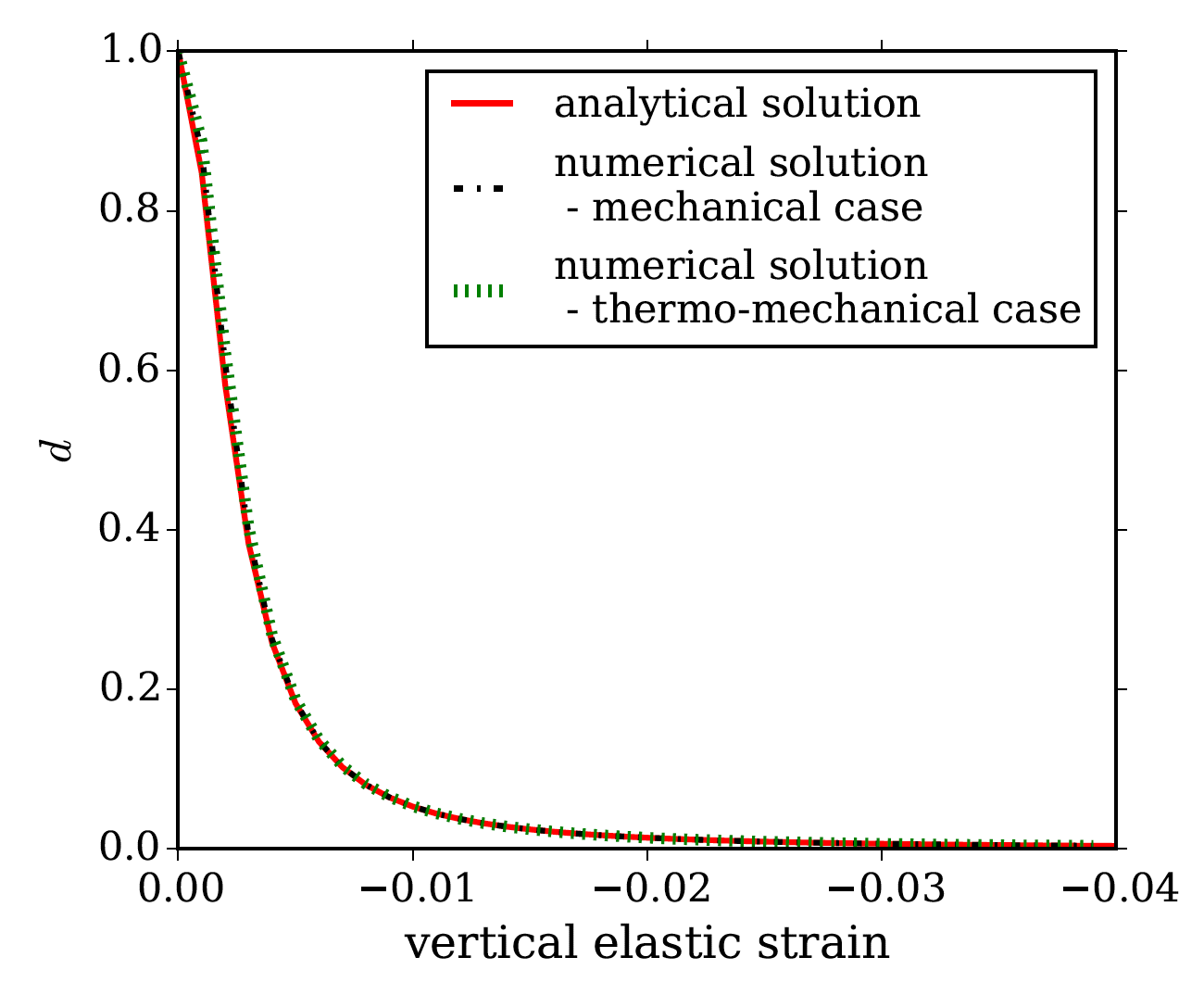
The analytical solution is:
$$d = \dfrac{G\textrm{c}}{G\textrm{c}+4\epsilon \psi_\textrm{e}^+}$$where due to negative (elastic) volume strains only the deviatoric energy drives the phase field.
$$ \begin{equation} \psi_\textrm{e}^+ = \mu \mathbf{\epsilon}^\textrm{D} : \mathbf{\epsilon}^\textrm{D} = \frac{2\mu}{3} \left(\frac{u(1+\nu)}{L} \right)^2 \end{equation} $$for mechanical case, and
$$ \begin{equation} \psi_\textrm{e}^+ = \mu \mathbf{\epsilon}^\textrm{D} : \mathbf{\epsilon}^\textrm{D} = \frac{2\mu}{3} [\alpha \Delta T(1+\nu)]^2 \end{equation} $$for thermo-mechanical case. Where the Poisson’s ratio is evolving with the degradation of the shear modulus
$$ \begin{equation} \nu(d) = \frac{3K-2Gd^2}{2(3K+Gd^2)} \end{equation} $$This article was written by Xing-Yuan Miao. If you are missing something or you find an error please let us know.
Generated with Hugo 0.122.0
in CI job 449919
|
Last revision: April 23, 2024
Commit: [PL/LD] Use generic cell average output 3557e29
| Edit this page on