Fluid flow through an open parallel-plate channel
Problem definition
This benchmark deals with fluid flow through an open parallel-plate channel. The figure below gives a pictorial view of the considered scenario.
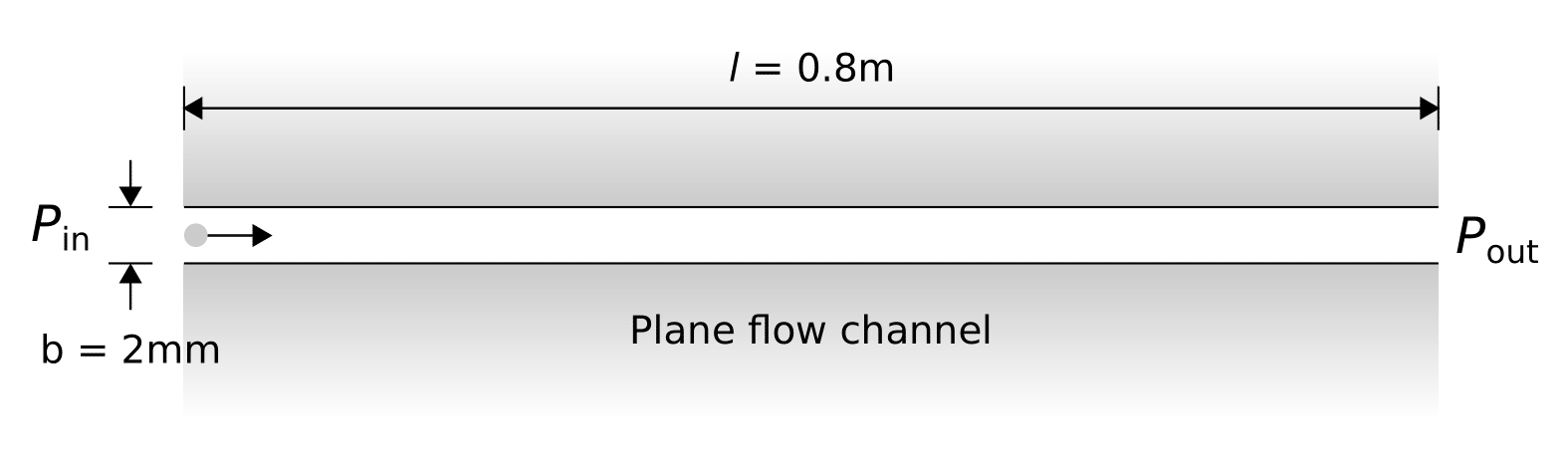
Schematic diagram of the parallel-plate flow channel in two-dimensional space.
The model parameters used in the simulation are summarized in the table below.
| Parameter | Unit | Value |
|---|---|---|
| Hydraulic pressure at the inlet $P_{\mathrm{in}}$ | Pa | 200039.8 |
| Hydraulic pressure at the outlet $P_{\mathrm{out}}$ | Pa | 200000 |
| Fluid dynamic viscosity $\mu$ | Pa$\cdot$s | 5e-3 |
Mathematical description
The fluid motion in the parallel-plate channel can be described by the Stokes equation. To close the system of equations, the continuity equation for incompressible and steady-state flow is applied. The governing equations of incompressible flow in the entire domain are given as (Yuan et al., 2016)
$$ \begin{equation} \nabla p - \mu \Delta \mathbf{v} = \mathbf{f}, \end{equation}$$\begin{equation} \nabla \cdot \mathbf{v} = 0. \end{equation}
Results
Figure 2(a) shows the hydraulic pressure profile through the parallel-plate flow channel, wherein the pressure drop is linearly distributed. Figure 2(b) gives the transverse velocity component profile over the cross-section of the plane flow channel which shows a parabolic shape. The transverse velocity component reaches a maximum value of 0.004975 m/s at the center which conforms to the value obtained from the analytical solution of the transverse velocity component. The analytical solution of the velocity is given as (Sarkar et al., 2004)
$$ \begin{equation} v \left(y\right) = \frac{1}{2\mu} \frac{P_{\mathrm{in}} - P_{\mathrm{out}}}{l} y \left( b - y\right). \end{equation}$$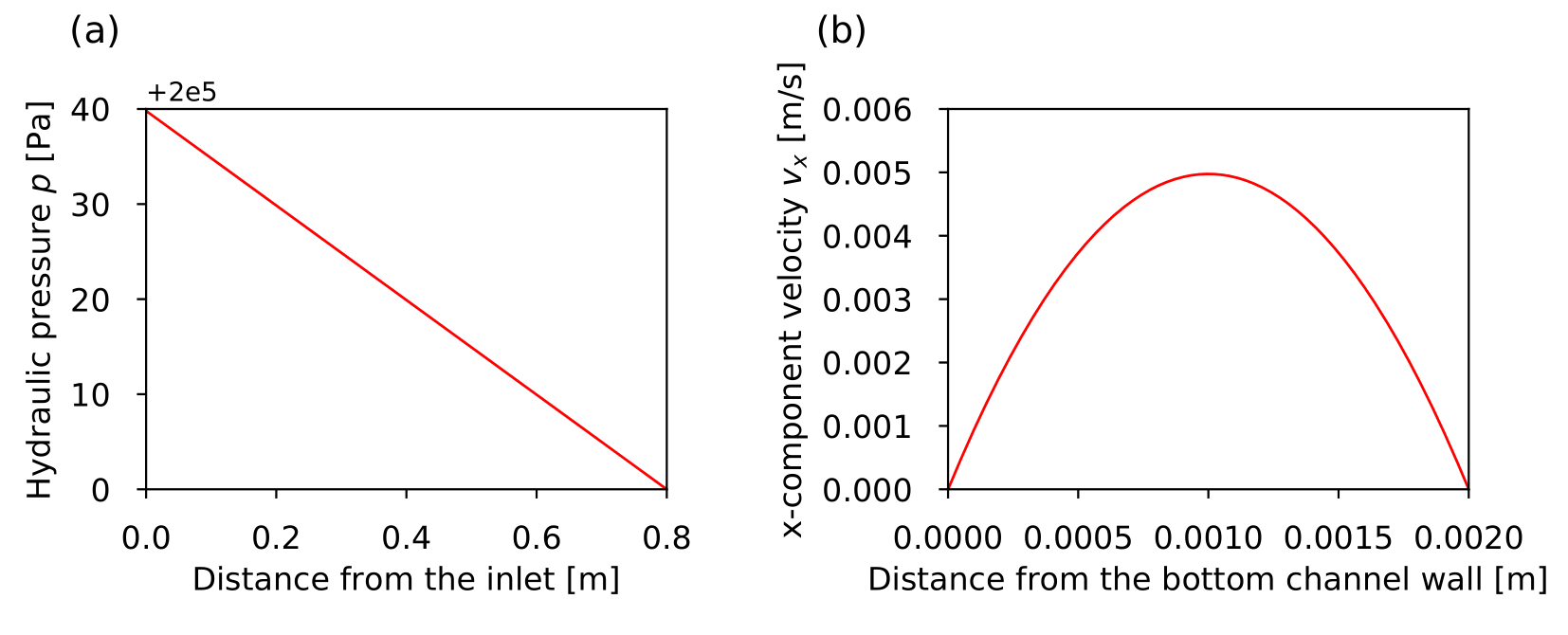
Simulation results: (a) Hydrualic pressure profile through the parallel-plate flow channel; (b) Transverse velocity component profile over the cross-section of the plane flow channel.
References
Sarkar, S., Toksoz, M. N., & Burns, D. R. (2004). Fluid flow modeling in fractures. Massachusetts Institute of Technology. Earth Resources Laboratory.
Yuan, T., Ning, Y., & Qin, G. (2016). Numerical modeling and simulation of coupled processes of mineral dissolution and fluid flow in fractured carbonate formations. Transport in Porous Media, 114(3), 747-775.
This article was written by Renchao Lu, Dmitri Naumov. If you are missing something or you find an error please let us know.
Generated with Hugo 0.122.0
in CI job 449919
|
Last revision: April 23, 2024
Commit: [PL/LD] Use generic cell average output 3557e29
| Edit this page on