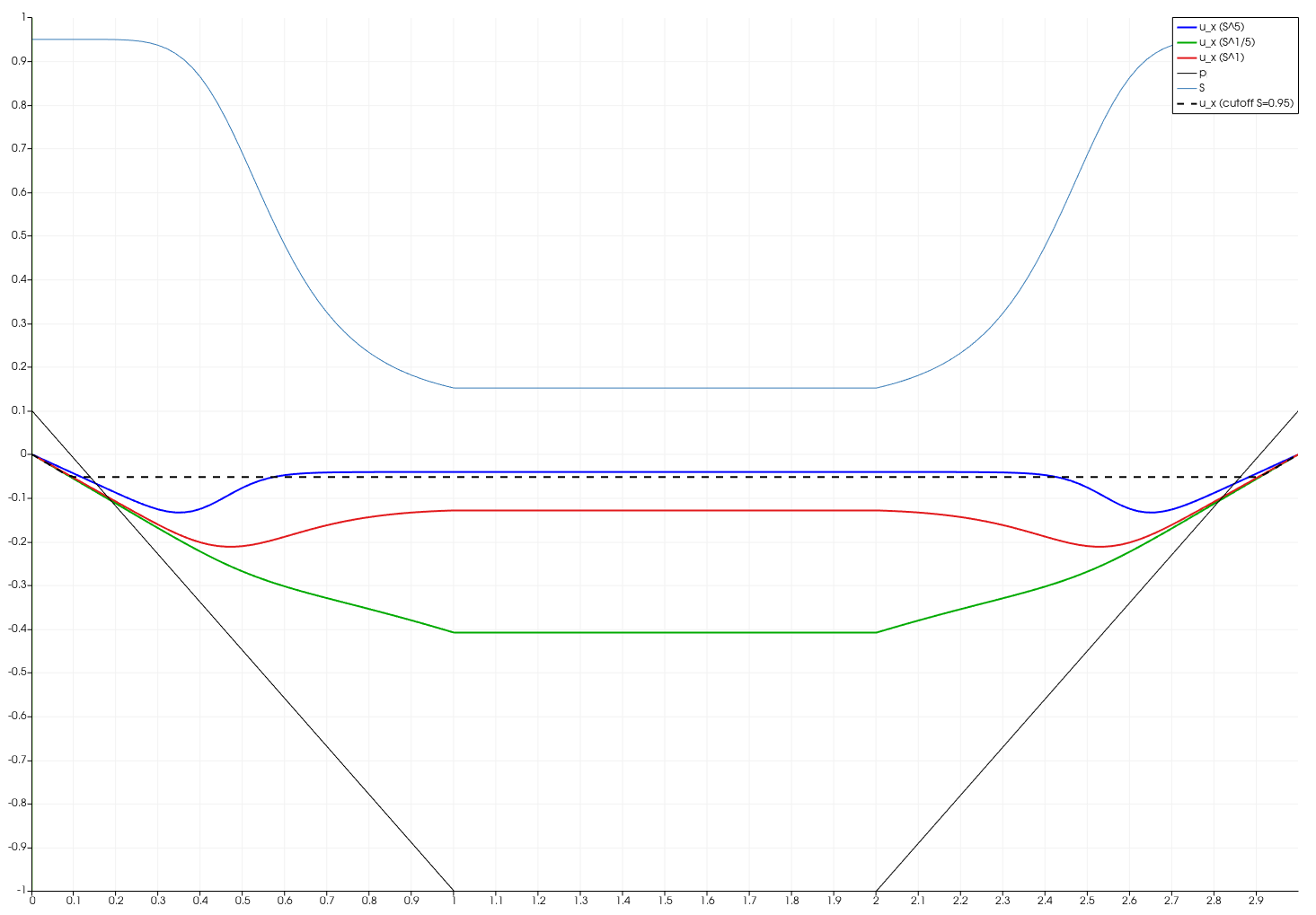
Bishop's effective stress models comparison
Two models for the Bishop’s effective stress computation are presented; the power-law model, and saturation cut-off model. The models are:
$$ \chi(S_\mathrm{L}) = S_\mathrm{L}^{m_\chi} \qquad \mbox{and}\qquad \chi(S_\mathrm{L}) = \chi = \begin{cases} 1 & \mbox{for $S_\text{L} \geq S_\text{cutoff}$} \\ 0 & \mbox{for $S_\text{L} < S_\text{cutoff}$.} \end{cases} $$
Simulation result shows different influence of the effective stress on the
displacement. In the test the medium is desaturated and then saturated again,
which causes shrinkage and expansion of the domain. Power law with exponents 1,
1/5, and 5 and saturation cut-off at maximum liquid saturation of 0.95 are
compared.
This article was written by Dmitri Naumov. If you are missing something or you find an error please let us know.
Generated with Hugo 0.122.0
in CI job 449919
|
Last revision: April 23, 2024
Commit: [PL/LD] Use generic cell average output 3557e29
| Edit this page on