Manufactured Solution for Laplace's Equation with Python

• Elliptic/square_1x1_SteadyStateDiffusion_Python/square_1e3_laplace_eq.prj

Motivation of this test case

The aim of this test is:

• to provide a simple introductory example of how Python BCs can be used
• to show that Python BCs can be used to easily prescribe BCs based on analytical formulas
• to check whether both essential and natural BCs are implemented correctly in OpenGeoSys’ Python BC.

Problem description

We solve Laplace’s Equation in 2D on a $1 \times 1$ square domain. The boundary conditions will be specified below.

Weak form

Laplace’s equation is

$$ \begin{equation} \- \mathop{\mathrm{div}} (a \mathop{\mathrm{grad}} u) = 0 \end{equation} $$

The weak form is derived as usual by multiplying with a test function $v$ and integrating over the domain $\Omega$:

$$ \begin{equation} \- \int_{\Omega} v \mathop{\mathrm{div}} (a \mathop{\mathrm{grad}} u) \, \mathrm{d}\Omega = 0 \,, \end{equation} $$

which can be transformed further to

$$ \begin{equation} \int_{\Omega} a \mathop{\mathrm{grad}} v \cdot \mathop{\mathrm{grad}} u \, \mathrm{d}\Omega = \int_{\Omega} \mathop{\mathrm{div}} (v a \mathop{\mathrm{grad}} u) \, \mathrm{d}\Omega = \int_{\Gamma_{\mathrm{N}}} v a \mathop{\mathrm{grad}} u \cdot n \, \mathrm{d}\Gamma \,, \end{equation} $$

where in the second equality Gauss’s theorem has been applied. As usual, the domain boundary $\partial\Omega = \Gamma\_{\mathrm{D}} \cup \Gamma\_{\mathrm{N}}$ is subdivided into the Dirichlet and the Neumann boundary and $v$ vanishes on $\Gamma\_{\mathrm{D}}$. The r.h.s. of the above equation is the total flux associated with $u$ flowing into the domain $\Omega$ through $\Gamma\_{\mathrm{N}}$: $-a \mathop{\mathrm{grad}} u$ is the flux density and $\-n$ is the inwards directed surface normal.

The weak form just derived is implemented (after FEM discretization) in the groundwater flow process in OpenGeoSys. Note that for the application of Neumann boundary conditions, it is necessary to know whether the flux has to be applied with a positive or a negative sign!

Analytical solution

The coefficient $a$ of Laplace’s equation is taken to be unity. By differentiation it can be easily checked that

$$ \begin{equation} u(x, y) = \sin(bx) \sinh(by) \end{equation} $$

solves Laplace’s equation inside $\Omega$ for any $b$. In this example we set $b = \tfrac 23 \pi$.

As boundary conditions we apply Dirichlet BCs at the top, left and bottom of the domain with values from $u(x,y)|\_{\Gamma_{\mathrm{D}}}$. On the right boundary of the domain a Neumann BC is applied. There $n = (1, 0)$, which implies that $a \mathop{\mathrm{grad}} u \cdot n = a \, \partial u / \partial x$.

Results

The numerical result obtained from OpenGeoSys is:

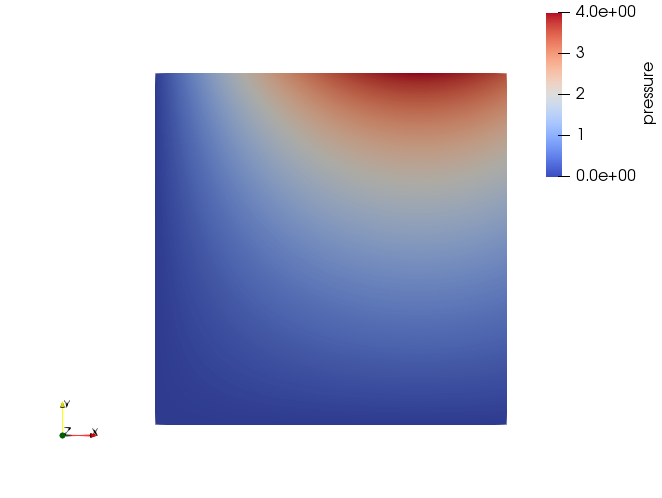
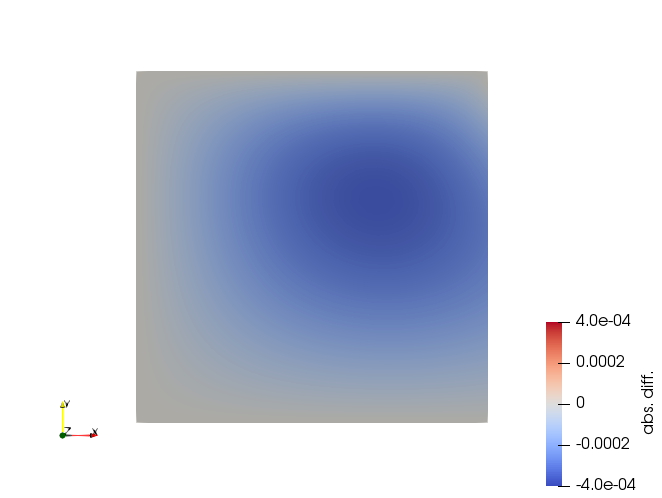
The absolute difference between the analytical and numerical solutions is smaller than $4 \cdot 10^{-4}$: