TCE Diffusion
In this benchmark, the steady-state diffusive transport of trichloroethylene (TCE) across a variably saturated zone (capillary fringe) is simulated and compared with the semianalytical solution proposed by Atteia and Höhener [1].
The model domain is 1-D in the vertical direction with a length of 1 m. The initial saturation profile is at steady state and shown in Fig. 1. The groundwater table is fixed at $z=0.407$ m by assigning a Dirichlet boundary condition of the gas pressure at $z=0$ m. The top boundary ($z=1$ m) is open with $P_g=101,325$ Pa. Initially, there is no TCE in the domain. A constant TCE molar fraction of $X^c=1\times10^{-6}$ is imposed below the water table (i.e. across the entire depth of the saturated zone), while null TCE concentration is assumed at the top boundary ($z=1$ m). A constant temperature of 298 K is maintained everywhere. The parameters of the numerical model are listed in Table 1.
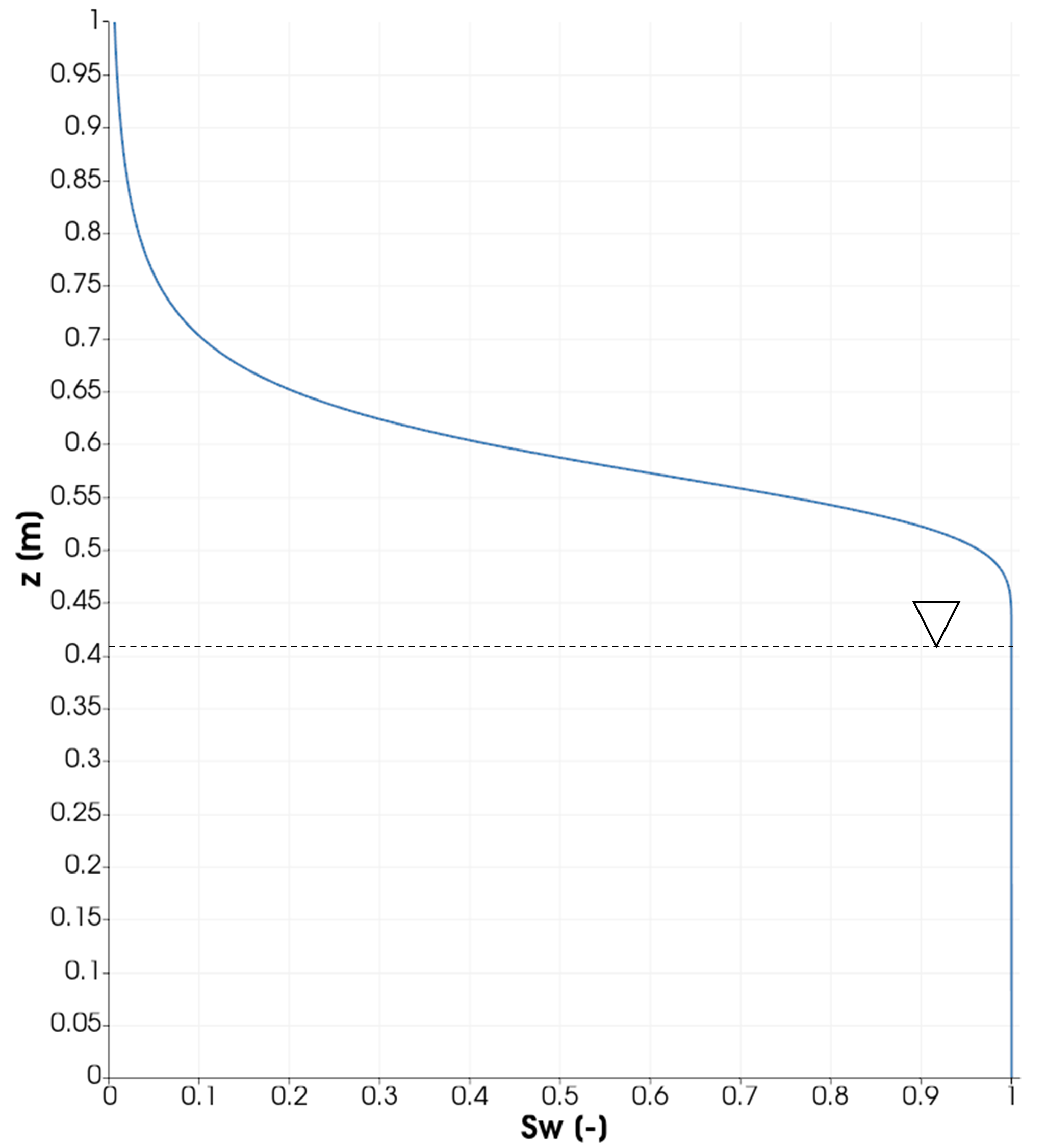
Initial saturation with depth.
Table 1: Parameters used in the numerical model.
| Parameter | Symbol | Value | Unit |
|---|---|---|---|
| TCE diffusion coefficient in free gas | $D_{0a}$ | $8.3\times10^{-6}$ | $\mathrm{m^2\ s^{-1}}$ |
| TCE diffusion coefficient in free water | $D_{0w}$ | $9.1\times10^{-10}$ | $\mathrm{m^2\ s^{-1}}$ |
| Henry’s Law constant | $H$ | $1.062\times10^{-3}$ | $\mathrm{mol\ m^{-3}\ Pa^{-1}}$ |
| Intrinsic permeability | $K$ | $1.18\times10^{-11}$ | $\mathrm{m^2}$ |
| Porosity | $n$ | 0.38 | - |
| Residual saturation | $S_r$ | 0 | - |
| van Genuchten parameter | $\alpha_{\mathrm{vG}}$ | 0.06 | $\mathrm{cm^{-1}}$ |
| van Genuchten parameter | $m_{\mathrm{vG}}$ | 0.8 | - |
Atteia and Höhener [1] developed a semianalytical solution for the TCE concentration profile at steady state. In their original solution, the effect of hydrodynamic dispersion is also considered. Here, we briefly derive a simplified semianalytical solution for the case without groundwater flow. By using the classical Millington [2] formulation for tortuosity, the diffusive flux in either phase $\alpha$ ($\alpha\in \{a, w\}$) can be written as
$$ J_{\alpha}=-nS_{\alpha}\tau_{\alpha}D_{0\alpha}\frac{dx^c_{\alpha}}{dz}=-n^{4/3}S_{\alpha}^{10/3}D_{0\alpha}\frac{dx^c_{\alpha}}{dz} $$in which $\tau_{\alpha}$ is the tortuosity of phase $\alpha$ and $x^c_{\alpha}$ is molar fraction of TCE in phase $\alpha$. Assuming equilibrium of contaminant concentrations between the liquid and gas phases, we have \begin{equation} \frac{N_wx^c_w}{P_gx^c_a}=H \end{equation} where $N_w$ is the molar density of water and $H$ is the Henry constant of TCE at the prescribed temperature (see Table 1). Thus, the total flux equals \begin{equation} J=J_a+J_w=-n^{4/3}\left(S_a^{10/3}D_{0a}+S_w^{10/3}D_{0w}HP_g/N_w\right)\frac{dx^c_a}{dz}=-A(z)\frac{dx^c_a}{dz}. \end{equation} By performing numerical integration, we have \begin{equation} x^c_a=c+J\cdot I(z)\ \mathrm{with}\ I(z)=\int\frac{1}{A(z)}dz. \end{equation} where $I(z)$ is integrated w.r.t. $z$ in the unsaturated zone. Since at steady state, the diffusive flux should be uniform at any depth, the integral constants $c$ and $J$ can be solved by the upper and lower values of $x^c_a$ which are given as Dirichlet boundary conditions. A MATLAB script is provided for the above solution.
Figure 2 compares the normalized gas phase TCE concentration profiles given by the numerical model and the above semianalytical solution at steady state. Figure 3 shows the absolute and relative errors between the two curves in Fig. 2. The maximum relative error is less than 1% except one point. Thus, a very good agreement was obtained. It is interesting to note the sharp decline of the TCE concentration immediately above the water table, which is due to the several orders of magnitude difference between $D_{0a}$ and $D_{0w}$.
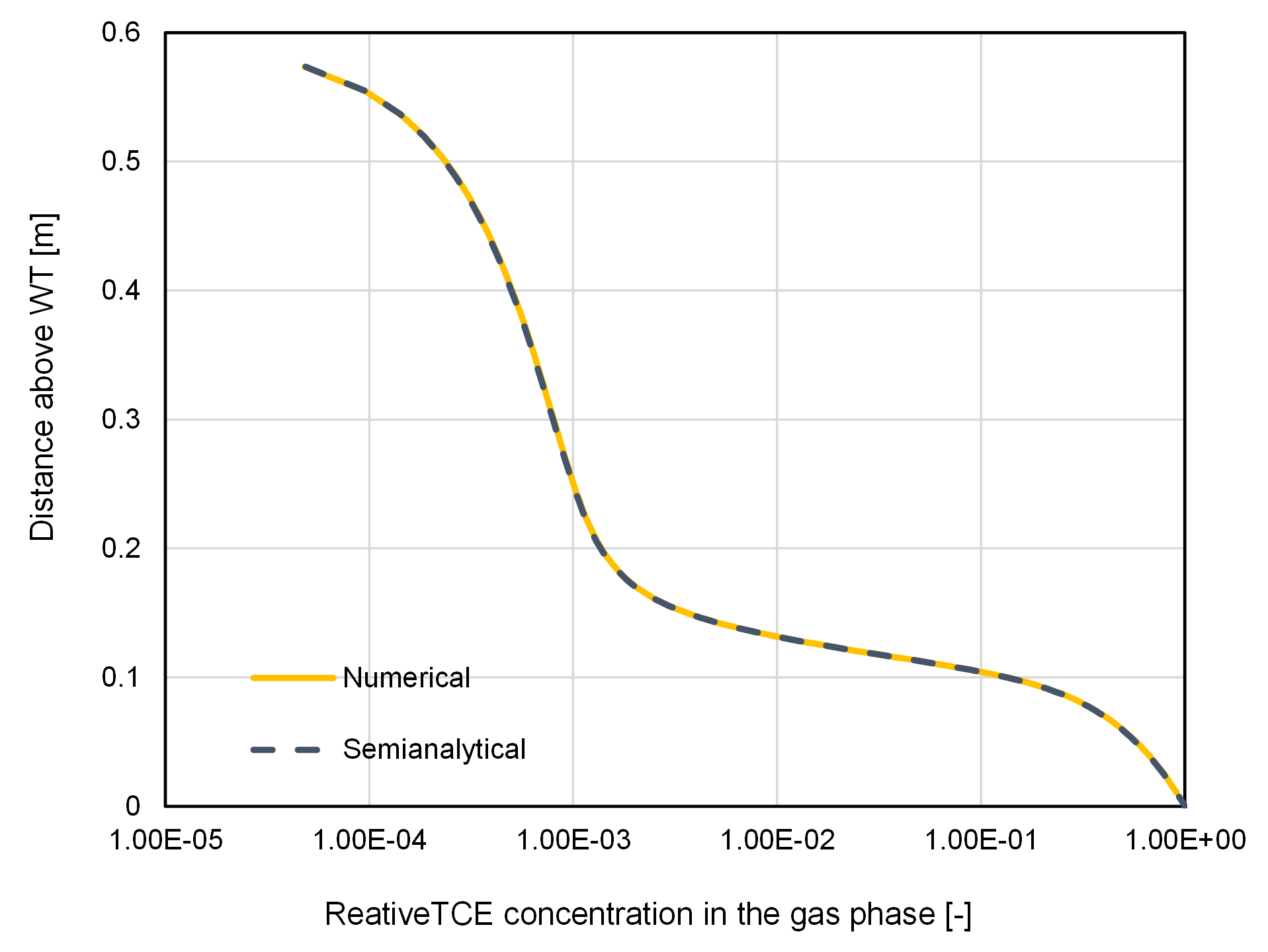
Comparison between numerical and semianalytical solutions.
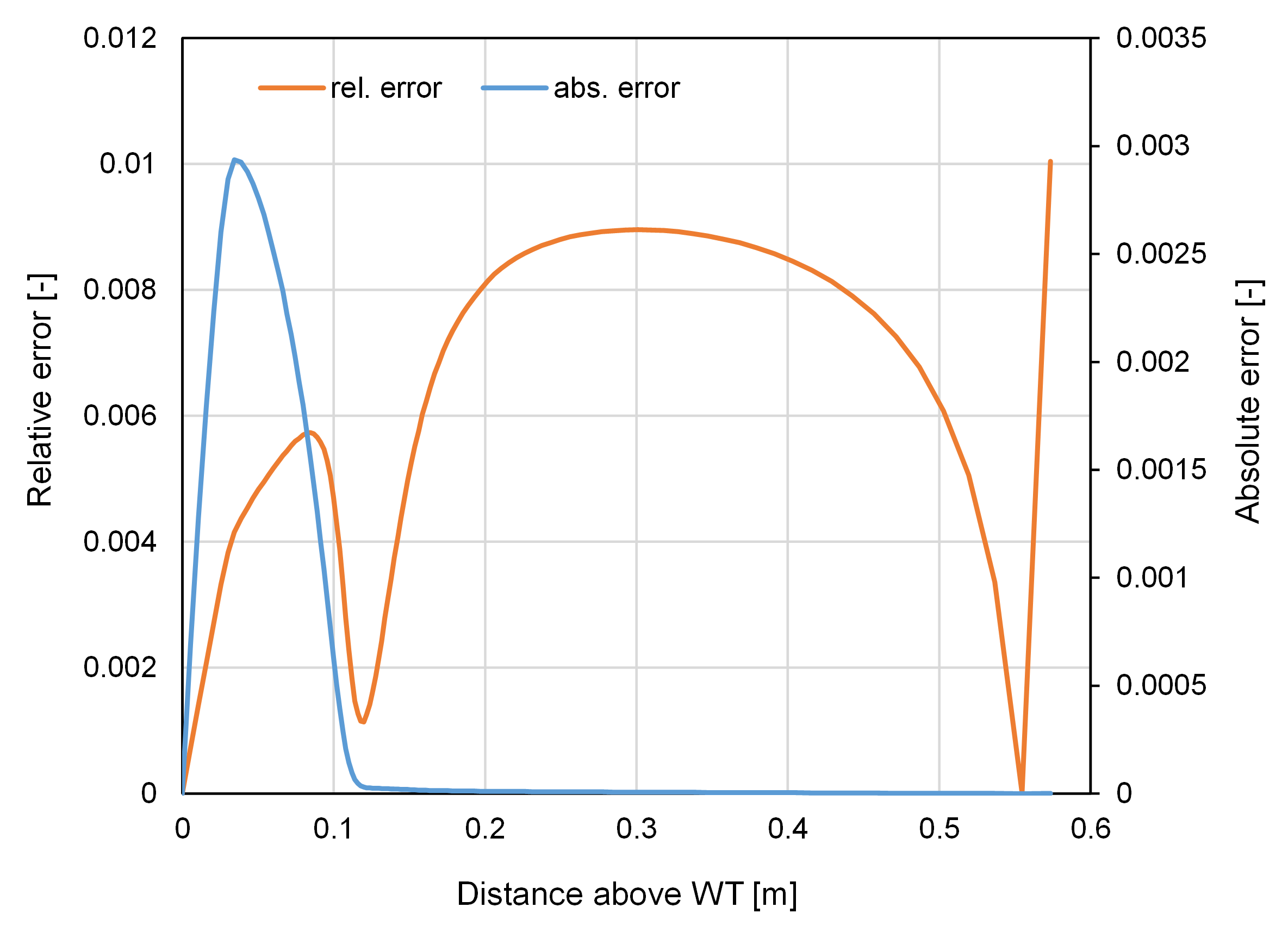
Absolute and relative errors.
References
[1] O. Atteia and P. Höhener. Semianalytical Model Predicting Transfer of Volatile Pollutants from Groundwater to the Soil Surface. Environmental Science & Technology 44 (16) (2010), pp. 6228–6232
[2] Millington, R. Gas Diffusion in Porous Media. Science 1959, 130, 100–102
This article was written by Boyan Meng. If you are missing something or you find an error please let us know.
Generated with Hugo 0.122.0
in CI job 570044
|
Last revision: April 17, 2025
Commit: Rewrite using ranges 1ed34f4
| Edit this page on